
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
逆采样(inverse transform sampling)是一种依赖于累积分布逆函数的采样方法
本文介绍逆采样的原理与具体执行方法,并展示一个具体的逆采样例子和具体代码实现
通过本文,可以了解什么是逆采样,如何使用逆采样,以及逆采样的代码实现方法
本节讲解逆采样的原理与方法,快速了解什么是逆采样
什么是逆采样
什么是逆采样
采样一般是指通过基本的伪随机数,来采集符合概率分布p(x)的样本
逆采样是一种"当p(x)的累积分布函数可逆时"的采样方法,具有简单、高效等优势
逆采样的采样流程如下:
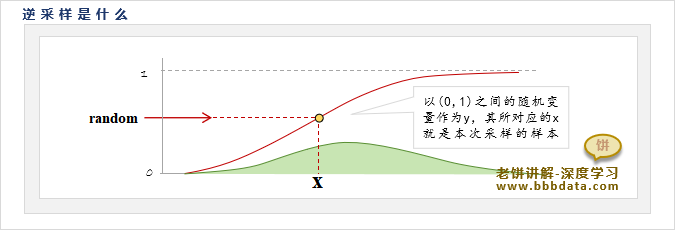
每次采样时,先生成一个(0,1)之间的随机数
然后以作为累积分布函数的,反求出作为采样样本,
即:
,其中,
例如生成的随机数为0.3,然后就可得到样本,逆采样在执行上非常高效
但逆采样的缺点是,条件要求苛刻,在实际中往往很难确切得到目标分布p(x)的“累积分布函数的逆函数”的
如何理解逆采样
逆采样的原理,可以通过离散采样来理解,示图如下:
离散采样就是先计算累积分布,再以随机数作为累积概率所对应的x作为本次采样
类似的,如右图所示,逆采样其实就是离散采样的连续形式,即以随机数作为累积概率所对应的x作为本次采样
本节展示一个逆采样的具体例子,以及代码实现
逆采样-例子与代码
下面通过一个具体例子,讲解如何进行逆采样,以及代码的实现
例如,假设需要采样的概率密度函数如下:
它的累积分布函数为:
累积分布的逆函数为:
则,每次采样时,先随机生成(0,1)之间的随机数
然后根据逆函数即可得到本次所需采样的x,即:
,
具体代码实现如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(999) # 设定随机种子
# ------ 逆采样 ------------
def cdf_inv(x): # CDF的逆函数
return np.log(1-x)**2 # 返回函数值
m = 20000 # 采样个数
x_sample = [] # 初始化采样结果
for i in range(m): # 逐个采样
y = np.random.rand() # 生成一个随机数
x = cdf_inv(y) # 计算当前的采样
x_sample.append(x) # 记录本次采样
#-----下面与逆采样算法无关,只用于统计采样的效果-------------
# -----------------采样效果验证----------------------
# 统计x_sample在每个区间的个数,比较x_sample的概率密度与p(x)的差异
def p(x): # 概率密度函数
return 1/(2*np.sqrt(x))*np.exp(-np.sqrt(x)) # 返回函数值
strip = 0.2 # 区间长度
r = [0,5] # 统计范围
x_stat = np.array(x_sample) # 复制一份x_sample
x_stat = x_stat[(x_stat>=r[0]) & (x_stat<=r[1])] # 只保留统计范围内的样本
bins = np.arange(r[0],r[1],strip) # 生成区间
bin_count = np.zeros(bins.shape[0]) # 初始化
bin_count[0] = sum(x_stat<=bins[0]) # 统计第一个区间
for i in range(bins.shape[0]): # 逐区间统计
bin_count[i] = sum((x_stat<=bins[i]) &(x_stat>bins[i-1])) # 统计当前区间的个数
stat = pd.DataFrame({'bins':bins,'cn':bin_count}) # 统计结果
stat['label'] = stat['bins']-strip/2 # 以区间中心作为标签
stat['p'] = (stat['cn']/stat['cn'].sum())/((r[1]-r[0])/bins.shape[0]) # 计算概率密度:区间个数占比/区间长度
plt.figure(figsize=(10, 3)) # 设置图片的大小
plt.bar(stat['label'], stat['p'],width=0.1,label='p-sample') # 画出柱状图
t = np.arange(r[0]+0.02,r[1],0.1) # 概率密度曲线的x
plt.plot(t,p(t),color='r', linestyle='-.',label='p(x)') # 画出概率密度曲线
plt.legend() # 添加图例
plt.show() # 展示画布运行结果如下:
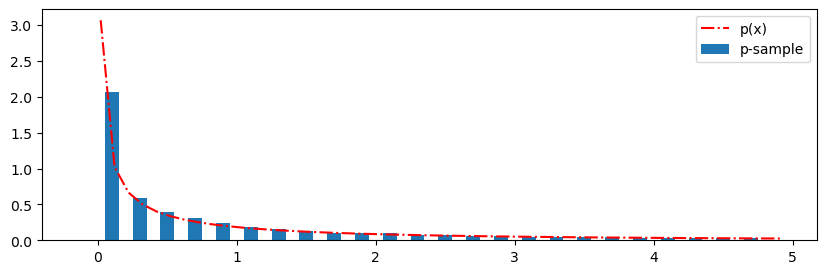
红色线是目标概率密度函数曲线p(x),而柱状图则是用逆采样的样本统计出来的密度分布
可以看到,通过逆采样获得的样本的分布密度与目标概率密度函数基本一致
好了,以上就是逆采样的介绍了以及代码示例了~
End
 评论
评论