
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
QR分解是一种矩阵分解方法,它把m×n的矩阵分解为列正交矩阵Q与上三角矩阵R的积
本节讲解QR分解的定义,并进一步讲述它的原理与分解流程,最后给出python实现QR分解的代码
通过本文,可以了解什么是QR分解,如何进行QR分解,以及它的分解原理和代码实现方法
本节讲解QR分解是什么和如何进行QR分解
QR分解的定义
对于列满秩矩阵A
可将其分解为列正交矩阵与上三角矩阵的积,
即
其中
👉 Q列与列之间两两正交
👉 R为非奇异上三角矩阵
QR分解的方法
符号说明
记的第i列为 ,Q的第i列为
即
Q的求法
Q中的求解如下
PASS
实际就是新的减去在各个之前已经正交化的上的投影分量,
从而得到由新 生成的新正交量
R的求法
在求得Q后,R可如下算得
✍️补充:关于Q的单位化
如果需要进一步单位化Q,
使Q的每一条列向量 为单位向量,
则可以在以上结果进一步如下单位化Q
Q的单位化公式
对应的R为
本节讲解上节所提供的QR分解公式的原理推导
相关引理
引理1:两条向量的正交
求b对a的正交向量d:
先求出b在a的投影向量c
则b对a的正交向量 为
引理2:与正交向量集的正交量
求 b对的正交量 d,使 d与都正交
其中, 是正交向量集,它的任意两条向量 正交
将 b可以减去在上的投影分量分量即可
其中
为b在上的投影分量
对于任意一个, d 都与正交,因为 中除了 和项,其余项都与正交,而b-k_ia_i又与a_i正交,所以d与a_i正交
即:
问题结论推导
Q的求法
因此,要用生成正交向量 ,
只需令,然后不断的用新的来生成与已有正交向量集的正交量即可
即可得到
....
R的求法
又由上,可得
...
即:
可知
3、单位化QR
可得,单位化的Q为:
对应的R为:
本节展示如何用python代码实现QR分解,并展示运行结果
python实现矩阵的QR分解
使用python实现QR分解只需按上述理论步骤进行即可
具体代码实现如下:
"""
代码说明:本代码用于实现-矩阵的QR分解
本代码来自《老饼讲解-机器学习》www.bbbdata.com
"""
import numpy as np
# 将矩阵进行QR分解
def QrDecompose(A):
#------------QR分解----------------------------
Q = np.zeros(A.shape) # 初始化Q
Q[:,0] = A[:,0] # A的第0列作为Q的第0列
R=np.identity(A.shape[1]) # 将R初始化为单位矩阵
for i in range(1,A.shape[1]): # 逐列计算Q、R
cur_beta = A[:,i].copy() # 初始化beta为Ai
for j in range(i): # 将Ai与Q[:,i-1]进行正交
k = A[:,i]@Q[:,j]/(Q[:,j].T@Q[:,j]) # 计算Ai在Qj的投影系数
R[j,i]= k # Rji就是Ai在Qj的投影系数
cur_beta -= k*Q[:,j] # 更新beta,令beta与Qj正交,即减去Ai在Qj的投影
Q[:,i] =cur_beta # 将最终的beta(即与Q[:,i-1]正交后的Ai)作为Qj
return Q,R
# 将QR矩阵进行单位化
def QrNormal(Q,R):
c = Q.shape[1] # Q的列数
D1 = np.zeros((c,c)) # 初始化对角矩阵D1
D2 = np.zeros((c,c)) # 初始化对角矩阵D2
for i in range(c): # 计算D的对角元素
D1[i,i] = np.sqrt(Q[:,i].T@Q[:,i]) # 计算D1的第i个对角元素,即|Q第i列|
D2[i,i] = 1/D1[i,i] # 计算D2的第i个对角元素,即1/|Q第i列|
nQ = Q@D2 # 计算单位化后的Q
nR = D1@R # 计算单位化后的R
return nQ,nR
# 测试样例
if __name__ == "__main__":
A = np.array([[1.,2.,5,8],[3.,5.,4,2],[6.,4,3,1]]).T # 生成需要QR分解的矩阵A
Q,R = QrDecompose(A) # 将A进行QR分解,得到列正交矩阵Q和上三角矩阵R
nQ,nR= QrNormal(Q,R) # 将QR进行标准化
#------------打印单位化前QR的信息--------------------
print("----原始数据A与分解后的QR---") # 打印矩阵A
print('A=\n',A) # 打印矩阵Q
print('Q=\n',Q) # 打印矩阵
print('R=\n',R)
print("\n-----用QTQ验证Q各个向量正交--") # 验证Q各个向量正交
QTQ= Q.T@Q # 计算QTQ
QTQ[np.abs(QTQ)<0.00001]=0 # 将过小的元素置0
print('Q^T*Q=\n',QTQ) # 打印QTQ
print("\n-----用A-QR验证A=QR--") # 验证A=QR
err = A-Q@R # 计算A与QR的误差
err[np.abs(err)<0.00001]=0 # 将过小的元素置0
print('A-QR=\n',err) # 打印误差
#----------单位化------------------------------------
print("\n----单位化后的QR:nQ,nR---") # 打印单位化后的QR
print('nQ=\n',nQ) # 打印单位化的Q
print('nR=\n',nR) # 打印单位化的R
print("\n-----用nQ^T*nQ验证nQ各个向量正交--") # 验证单位化的结果
nQTnQ= nQ.T@nQ # 计算nQTnQ
nQTnQ[np.abs(nQTnQ)<0.00001]=0 #
print('nQ^T*nQ=\n',nQTnQ) #
print("-----用A-QR验证A=QR--") #
nerr = A-nQ@nR #
nerr[np.abs(nerr)<0.00001]=0 #
print('A-nQ*nR=\n',nerr) # 代码运行结果如下:
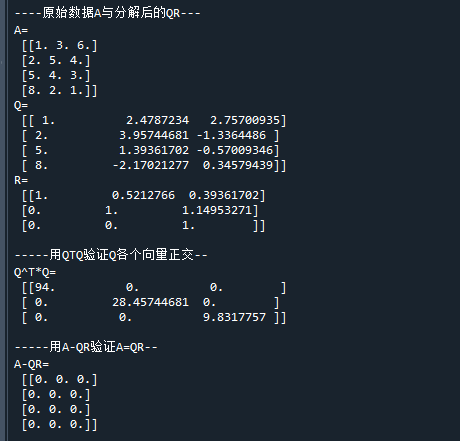
好了,以上就是矩阵的QR分解以及代码实现了~
End
 评论
评论