
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
GRU (Gated Recurrent Unit)循环神经网络是一种使用GRU门控循环单元来作为隐神经元的神经网络
本文讲解GRU神经网络的原理,以及GRU神经网络的具体结构,并展示GRU神经网络的代码实现例子
通过本文,可以快速了解GRU循环神经网络是什么,有什么特点,以及如何使用GRU神经网络来解决序列预测问题
本节讲解GRU循环神经网络的模型结构,以及计算公式
GRU循环神经网络-模型结构
GRU神经网络是一种使用门控循环单元 (Gated Recurrent Unit)作为隐神经元的循环神经网络
GRU出自2014年论文:《Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation》
简单来说,GRU也是一种可以具有长短期记忆的循环神经网络,只是它比LSTM更加简洁,因此受到青睐
GRU神经网络的结构如下:
一般所说的GRU神经网络就是指用GRU的CELL来替代经典RNN所得到的循环神经网络
GRU在t时刻隐节点的输出的计算公式如下:
其中分别称为重置门与更新门,是激活函数
计算公式如下:
重置门:
更新门:
备注:神经元激活函数一般取为tanh函数,门激活函数一般取为sigmoid函数
GRU神经网络公式理解
下面对GRU每步计算过程进行解读
👉第一步:输入的计算
GRU的输入计算公式如下:
GRU输入的计算公式与经典RNN相似,只是加入了重置门来控制是否使用上一时刻的隐节点信息
如果重置门趋于0,则代表重置了隐层的信息,使用的是当前时刻的输入信息
👉第二步:隐神经元输出的计算
隐神经元的计算公式如下:
可以理解为"本次输入",而则是上次的隐神经元
所以GRU可以理解为,用以权重来更新之前的隐神经元
本节解讲GRU神经网络的公式以及GRU的设计原理
GRU神经网络模型原理
GUP神经网络的原理
GRU相当于借鉴LSTM"门控"的思想来解决长短期问题(既能使用长期信息,又能使用短期信息)
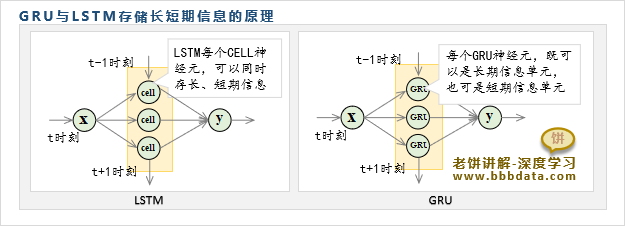
在LSTM中,一个CELL单元既存了长期信息,也存了短期信息,以此来解决长短期问题
而GRU则是:"一个GRU单元既可以是一个存储短期信息的单元,也可以是存储长期信息的单元"
备注:上述说法并非是严谨的,只是这样子来更容易理解GRU和LSTM的模型原理
那么,整个隐层中有部分单元存储了长期信息,有部分存储了短期信息,这样输出就可以同时利用长短期信息
一、GRU单元如何充当一个存储短期信息的神经元
如果当前神经元存储的是短期信息,那么重置门应该是连续活跃的,而更新门不活跃
不妨极端点设,这样GRU的公式就变为:
也就是经典RNN了,隐神经元H中以短期信息为主
二、GRU神经元如何充当一个存储长期信息的神经元
如果当前单元存储的是长期信息,那么自从信息输入后,更新门就连续活跃
不妨极端点设,这样GRU的公式就变为:
也就是自信息输入后,该隐节点的信息一直不变地延续到之后的节点
上面虽是以极端情况为例,但可以说明,GRU单元既可以是一个存储短期信息的单元,也可以是存储长期信息的单元
本节展示如何使用GRU来解决序列预测问题,以及GRU的代码实现
GRU神经网络-代码实现
实现GRU与实现RNN是一样的,只需将隐神经元替换为GRU就可以了
下面的例子与RNN一文中的问题是一样的,代码也几乎一样,只是隐层使用了GRU神经元
如图所示,以下是一个sin函数的曲线与序列数据,我们希望通过前5个数据预测下一个数据
我们将数据处理为以下的形式:
x1-x5是t时刻之前的5个数据,y是本时刻的数据,我们使用x1-x5来预测y
我们设计一个Nv1的RNN模型(使用GRU隐神经元)如下:
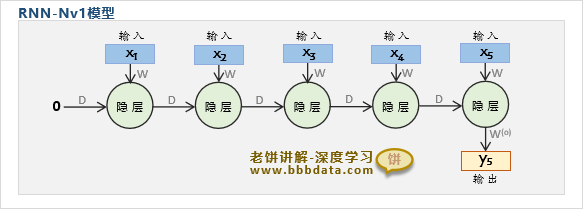
它的意义就是,将前5个时刻的X按顺序更新到隐节点,再用承载了所有输入信息(x1-x5)的隐节点来拟合输出y
下面我们使用pytorch来实现上述所设计的模型,以及训练模型
具体实现代码如下:
import torch
import random
import torch.nn as nn
import matplotlib.pyplot as plt
# ----------------------数据生成--------------------------
data = torch.sin(torch.arange(-10, 10,0.1)) # 生成sin序列数据
plt.plot(data)
seqLen = 5 # 利用前5个时刻预测下一时刻
sample_n = len(data)-1-seqLen-1 # 样本个数
x = torch.zeros(seqLen,sample_n,1) # 初始化x
y = torch.zeros(1,sample_n,1) # 初始化y
for i in range(sample_n): # 从序列数据中获取x与y
x[:,i,:] = data[i:i+seqLen].unsqueeze(1) # 将前5个数据作为x
y[:,i,:] = data[i+seqLen] # 将下一个数据作为y
valid_sample_n = round(sample_n*0.2) # 抽取20%的样本作为验证样本
idx = range(sample_n) # 生成一个序列,用于抽样
valid_idx = random.sample(idx, valid_sample_n) # 验证数据的序号
train_idx = [i for i in idx if i not in valid_idx] # 训练数据的序号
train_x = x[:,train_idx,:] # 抽取训练数据的x
train_y = y[:,train_idx,:] # 抽取训练数据的y
valid_x = x[:,valid_idx,:] # 抽取验证数据的x
valid_y = y[:,valid_idx,:] # 抽取验证数据的y
#--------------------模型结构----------------------------------
# RNN神经网络的结构
class RnnNet(nn.Module):
def __init__(self,input_size,out_size,hiden_size):
super(RnnNet, self).__init__()
self.rnn = nn.GRU(input_size, hiden_size)
self.fc = nn.Linear(hiden_size, out_size)
def forward(self, x):
h,_ = self.rnn(x) # 计算循环隐层
h = h[-1,:,:].unsqueeze(0) # 只需要最后一个时刻的隐节点
y = self.fc(h) # 计算输出
return y,h
#--------------------模型训练-----------------------------------
# 模型设置
goal = 0.0001 # 训练目标
epochs = 20000 # 训练频数
model = RnnNet(1,1,10) # 初始化模型,模型为1输入,1输出,10个隐节点
lossFun = torch.nn.MSELoss() # 定义损失函数为MSE损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 初始化优化器
# 模型训练
for epoch in range(epochs):
optimizer.zero_grad() # 将优化器里的参数梯度清空
train_py,_ = model(train_x) # 计算模型的预测值
train_loss = lossFun(train_py, train_y) # 计算损失函数值
valid_py,_ = model(valid_x) # 计算模型的预测值
valid_loss = lossFun(valid_py, valid_y) # 计算损失函数值
if(epoch%1000==0):
print('------当前epoch:',str(epoch),'----------') # 打印当前步数
print('train_loss:',train_loss.data) # 打印训练损失值
print('valid_loss:',valid_loss.data) # 打印验证损失值
if(train_loss<goal): # 如果训练已经达到目标
break # 则退出训练
train_loss.backward() # 更新参数的梯度
optimizer.step() # 更新参数
# ------------------展示结果--------------------------------------
py,_ = model(x) # 模型预测
loss= lossFun(py, y).data # 打印损失函数
print('整体损失值:',loss)
plt.figure() # 初始化画布
plt.plot( y[0,:,0], color='r', linestyle='-.',label='true_y') # 绘制真实曲线
plt.plot( py[0,:,0].detach(), color='b', linestyle='-.',label='predict_y') # 绘制预测曲线
plt.legend(loc=1,framealpha=1) # 展示图例
plt.show() # 展示图像运行结果如下:
------当前epoch: 0 ----------
train_loss: tensor(0.3251)
valid_loss: tensor(0.3268)
------当前epoch: 1000 ----------
...
train_loss: tensor(0.0004)
valid_loss: tensor(0.0004)
------当前epoch: 19000 ----------
train_loss: tensor(0.0003)
valid_loss: tensor(0.0003)
整体损失值: tensor(0.0002)
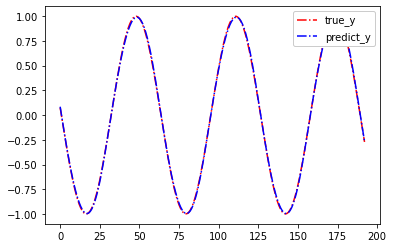
可以看到,模型整体的损失值(MSE)已经极小,所预测的y与真实y已经几乎完全一样
好了,以上就是GRU门控单元循环神经网络的原理和使用示例了~
End
 评论
评论