
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
ID3决策树是罗斯.昆兰(J. Ross Quinlan)于1975年提出的一种基于信息增益函数的决策树模型
本文讲解ID3决策树的模型结构、模型思想原理,以及ID3决策树的算法流程
通过本文,可以快速了解ID3决策树模型是什么,以及ID3决策树的相关公式的具体意义
前言
ID3算法是相对较早的算法,现在已经一般都不使用了,而是使用CART决策树
但ID3作为一个经典算法,仍然有独特的、闪光的地方
本文讲解ID3算法是什么,包括它的思想、模型结构以及相关公式
由于一般的软件已经不实现ID3,实际中也很少使用
因此本文不提供代码实现,事实上也不建议大家花太多时间在ID3决策树上面
备注:本文需建立在CART决策树的认识上再进行阅读,阅读时注意ID3与CART的区别
本节讲解ID3决策树模型是什么,并与CART决策树进行对比
ID3决策树模型
ID3是最早的决策树模型算法,由罗斯.昆兰(J. Ross Quinlan)于1979年提出
ID3决策树模型简单而朴素,它模仿人类的决策方式,用于解决模式识别(分类)问题
ID3决策树模型如下:
ID3决策树模型与CART决策树一样,都是一棵树,但它的输入变量必须全是枚举型
它在每个节点都选择一个变量,然后按变量的所有取值可能进行分枝
如图所示,一棵ID3决策树由3部分构成:
1. 节点选择哪个变量分枝
2. 节点是否能成为叶子节点
3. 如果是叶子节点,该叶子节点的属于哪一类
ID3与CART树的比较
下面不妨通过ID3决策树与CART决策树的比较,来进一步加深对ID3决策树的理解
ID3与CART决策树的模型结构差异如下:
1. 变量类型
CART的输入是连续变量,ID3的输入变量是枚举变量
2. 分叉类型
CART决策树是一棵二叉树,即每次只作二分叉
而ID3是全分叉,它对节点变量的枚举值全分叉,变量有多少个枚举值就分多少个叉
所以CART需要指定分裂阈值,而ID3并不需要,因为它是全分裂
3. 层数上限
CART如果在第一层选择了身高变量分叉,那第二层,仍然可以选择身高来分叉
而ID3如果在第一层选择了身高,那第二层只能选择身高以外的变量来分叉,即变量不可重复
因此,CART可能会有很多层,因为它的变量可重复利用,而ID3的层数必定<=变量个数
4. 变量分叉点
CART在确定节点所选择的变量后,还需要确定变量的分割阈值,根据阈值来分叉
而ID3不需要,它直接按变量枚举个数进行全分叉,因此它不需要阈值
一句话总结:相比CART, ID3更原始、简单、粗爆,它就是枚举变量全分叉
本节介绍ID3决策树分叉时使用的评估函数
ID3的分叉评估函数
ID3每次分叉时,需要确定选择哪一个变量,因此需要一个函数来评估分叉质量
在ID3算法中,使用信息增益作为分叉质量评估函数
信息增益(Gain)函数如下:
其中,
:分叉子节点个数
:所有子节点的总样本数(也即父节点的样本数)
:第 i 个子节点上样本个数
:第 i 个子节点上第k类样本的个数
:父节点上第 k 类样本的个数
信息增益的意义是,分叉后比分叉前信息量(不确定性)的减少量
信息增益函数的推导
ID3的信息增益(Gain)函数的意义就是,分叉后比分叉前信息量(不确定性)的减少量
信息增益函数的详细推导如下:
1. 节点分类质量
度量单个节点上的分类质量可以用经验熵公式:
其中
:节点上样本个数
:节点上样本的类别个数
:节点上属于 k 类的样本个数
说明:熵的背景意义是不确定性
所以,H越大,代表该节点越不能确定它是哪一类,越大质量就越差
2. 分叉质量
分叉质量 (信息增益)= 分叉前质量 - 分叉后质量
分叉前质量:分叉前是一个单节点,直接用单节点的经验熵即可
分叉后质量:用各个分叉子节点的经验熵加权和(也称为条件经验熵)即可
其中,
:子节点个数
:所有子节点的总样本数
:第 i 个子节点上样本个数
:第 i 个子节点上第k类样本的个数
两者相减(分叉前质量 - 分叉后质量)就得到了分叉带来的质量提升--信息增益
本节讲解ID3的整体算法流程
ID3决策树-算法流程
算法基本是用贪婪算法,即从根节点,逐个逐个节点向下分裂,
每次只要确定分裂哪个变量,分裂之后节点是否还要继续分裂即可
ID3算法主流程
ID3算法主流程如下: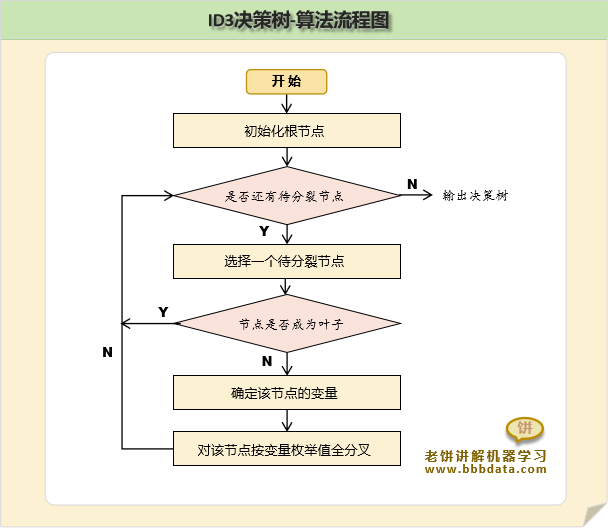
1. 计算各个变量的信息增益,确定本次由哪个变量分支
2. 对变量分支后,确定哪些节点是叶子节点
哪些需要再分,需要再分的就继续由剩余变量分支
3. 如果所有节点都不需分支,或所有变量已分完,则停止算法
其中,成为叶子节点的条件如下:
(1) 该节点按最优秀的变量去分,收益仍然极小
则该节点不再分,作为叶子节点
(2) 无变量可分
(3) 叶子上的样本全属于同一类
叶子节点的类别如下确定:
叶子节点的样本中,哪个类别的样本最多,则节点就是哪个类别
好了,以上就是ID3决策树的算法流程与相关公式了~
End
 评论
评论