
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
广义回归神经网络GRNN是D.F.Specht在1991年提出的一种径向基神经网络,适用于回归问题
本文讲述广义回归神经网络GRNN的原理、模型表达式、结构拓扑,并展示如何在matlab中实现一个GRNN
通过本文,可以快速了解什么是广义回归神经网络,它是思想是什么,以及如何使用GRNN解决回归问题
本节讲解广义回归神经网络GRNN解决回归问题的思路
什么是广义回归神经网络
广义回归神经网络GRNN全称为General Regression Neural Network,用于解决回归问题
它是D.F.Specht在1991年提出的一种神经网络,与径向基神经网络有异曲同工之处
GRNN是如何解决回归问题的
设有已知y 值的历史样本 x1,x2,如果新来了一个样本 x,那 x 的 y 值为多少?
广义回归解决该问题的思路如下:
它假设x与任何一个已有样本中相同的概率都服从正态分布
则易知,样本与样本相同的概率为 :
样本与样本相同的概率为 :
取两者y的概率加权和来预测x,则有:
简单来说,广义回归的思想就是评估新样本属于各个训练样本点的概率各是多少
然后以概率加权得到新样本的输出值评估
本节讲解广义回归神经网络的模型表达式以及构建方法
广义回归神经网络的数学表达式
广义回归神经网络的数学表达式
这里我们不写通用公式,只以具体例子说来说GRNN模型的数学表达式
一个2输入、3个样本的GRNN神经网络的数学表达式如下:
其中,b是待定超参数,它决定了径向基的宽度
Esum是所有径向基函数之和 ,如下:
✍️ 实际Esum的作用是把各个径向基的值进行归一化,将径向基转为权重
广义回归神经网络的拓扑结构
广义回归神经网络是一个固定的三层神经网络, 它的拓扑图如下
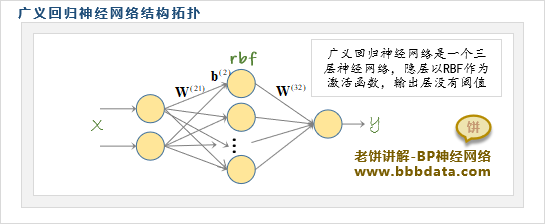
广义回归神经网络的网络拓扑图与径向基神经网络是一致的,只是输出层没有阈值
广义神经网络的构建
从广义回归神经网络的数学表达式可以知道
广义回归神经网络是最简单的神经网络,不需要任何计算,就能将网络构建出来
GRNN只需要把训练样本的 X , y 保存起来,并设置好隐层的阈值 的值(即公式中的b)就可以了
来了新样本,只要按上述表达式来计算预测值就可以了,即它是一个生成模型,整个构建过程不需任何训练
GRNN与RBF的差异比较
广义回归神经网络虽然名字里没有带有“径向基”字样,但它的传递函数用的就是径向函数
所以广义回归神经网络实际上仍然属于径向基神经网络的一种
下面我们将其与RBF径向基神经网络进行辨识与比较
一、相同之处
1. 数学表达式上有相似的形式
2. 隐节点同样是径向函数
二、不同之处
1. RBF是通过曲线拟合的思想,而GRNN是通过概率加权的思想
2. RBF需要训练参数,而GRNN是生成模型,不需要训练
3. RBF外层有阈值,GRNN外层没有阈值
4. 特别的是,GRNN的隐节点(exp部分)需要归一化,再与外层权重相乘
本节讲解如何使用matlab实现一个广义回归神经网络
GRNN代码实现
在matlab中使用newgrnn来构建一个广义回归神经网络,用于解决回归问题
具体代码如下:
%代码说明:径向基newgrnn的matlab工具箱使用Demo
%来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2014b
%-----------------------------------------------------
%----数据准备----
x1 = 1:0.2:10;
x2 = -5:0.2:4;
X = [x1;x2]; % 输入数据,注意中间是分号
Y = sin (X(1,:))+X(2,:); % 输出数据
%----网络训练----
net = newgrnn(X,Y,1); % 网络建立与训练,第三个参数用于控制径向基的宽度
simY = sim(net, X); % 用建好的网络预测原始数据
%----结果对比----
figure(1);
t = 1:size(Y,2);
plot(t,Y,'*',t,simY,'r') 代码运行结果如下:
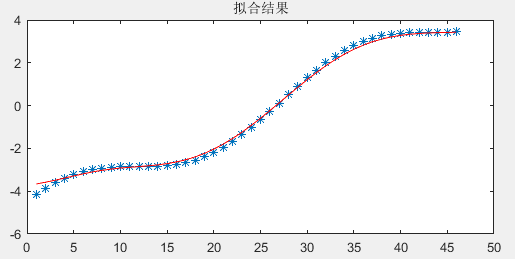
可以看到,模型基本拟合了原本的数据样本点
好了,以上就是广义回归神经网络GRNN的入门与使用了~
End
 评论
评论