
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
Lasso回归全称为Least absolute shrinkage and selection operator,是一种可用于筛选变量的模型
本文讲解Lasso回归的模型表达式、损失函数以及Lasso回归的原理与意义,并展示一个Lasso回归的实现例子
通过本文,可以快速了解Lasso回归是什么,模型的原理是什么,以及如何使用Lasso回归来进行筛选变量
本节讲解Lasso回归模型是什么,包括Lasso回归的表达式、损失函数与求解方法等
Lasso回归模型是什么
Lasso回归模型简单来说,就是在线性回归模型的基础上,加入一范正则项
虽然Lasso回归是一个回归模型,但由于它具有系数稀疏化的特点,因此也常用于筛选变量
Lasso的模型表达式如下:
Lasso回归的损失函数如下:
其中,:样本个数
:系数个数
:y的预测值
:y的真实值
:惩罚系数,用于调节系数W的惩罚力度
Lasso回归模型的阈值
与岭回归模型一样,原始的Lasso回归模型是不带阈值的
因为Lasso回归的目的是对各个w进行惩罚,而阈值b是不需要惩罚的
因此,Lasso回归一般先对数据进行中心化,再进行建模,再反求出阈值,如下:
(1) 先将数据作中心化转换:
此时, 都是以(0,0)为中心的数据
(2) 用训练Lasso回归模型, 得到
(3) 训练后再计算阈值b:
即可得到
本节讲解Lasso回归是如何训练的,以及Lasso回归为什么可以得到稀疏化系数
Lasso回归的模型训练
由于Lasso以L1范数作为正则项,无法得到公式解,一般用坐标下降法进行求解
坐标下降法每次都保持其它参数不变,只将其中一个参数调整到最优解(即驻点)
以上述方式进行反复迭代,直到参数的变化很小或达到最大迭代次数则终止训练
Lasso的求解流程如下:
1. 初始化解全为 0
2. 循环迭代, 每次将一个w调整为最优w(可按顺序选择w,也可随机)
最优w的求法:求损失函数对该w的导数,令导为0,即可求得最优w
3. 直到满足终止训练条件,退出迭代
终止条件为:(1)达到最大迭代次数,(2)w的变化率极微小
Lasso回归模型的意义-系数稀疏化
Lasso是对线性回归、岭回归的改进,它令系数正则化的同时,尽量使系数稀疏化
Lasso回归与系数稀疏化
在变量多重共线性的时候,我们往往希望模型在足够有效的前提下,能够使用越少的变量越好
例如,当时,我们希望得到的模型表达式为 ,而不是
这种能令部分系数为0的效果,就被称为系数稀疏化,它可以起到简化模型或者筛选变量的作用
为什么Lasso回归容易让系数稀疏化
岭回归虽然能够抑制系数过大,但它很难得到稀疏系数,而Lasso回归却比较容易得到稀疏系数
非严谨解释如下:
不妨把损失函数中的误差项记为 ,正则项记为 ,则此时损失函数简记为
可证明,损失函数 的最优解必定在 的等高线与 的等高线的切点处取得(这里省略证明)
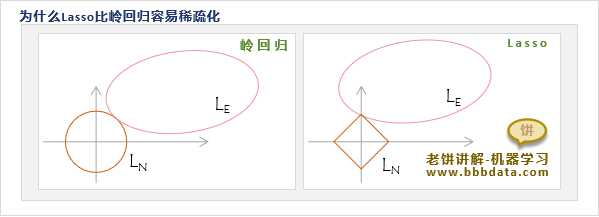
以二维为例,岭回归的正则项是一个圆,要与相切于坐标轴是很难的
反观Lasso的正则项 ,它是一个棱形,要与相切于坐标轴却很容易
因此,岭回归很难得到稀疏系数,而相比之下,LASSO回归更易得到稀疏系数
正因为LASSO回归容易得到稀疏系数,因此也可作为筛选变量的一种技术
在建模之前,可以先用Lasso回归检测哪些变量的系数为0,然后把系数为0的变量去掉再进行建模
本节展示如何实现一个Lasso回归模型,并展示如何利用Lasso排除冗余变量
Lasso回归代码实现
在sklearn中要实现Lasso回归,只需调用linear_model.Lasso就可以
具体代码如下:
"""
LASSO 回归
"""
from sklearn.linear_model import Lasso
import numpy as np
# ======生成数据=========
x1 = np.arange(0,100) # 生成x1
x2 = x1*4+3 # 生成x2,这里的x2与x1是线性相关的
x = np.concatenate((x1.reshape(-1, 1),x2.reshape(-1, 1)),axis=1) # 将x1,x2合并作为x
y = x.dot([2,3]) # 生成y
# =====Lasso模型训练========
alpha =0.3 # 设置正则项系数alpha
mdl = Lasso(alpha=alpha,fit_intercept=True,tol=1e-4,max_iter=1000) # 初始化Lasso回归模型
mdl.fit(x,y) # 用数据训练模型
sim_y= mdl.predict(x) # 预测
# ================= 打印结果 =======================
print('\n======Lasso训练结果==================')
print('权重:'+str(mdl.coef_))
print('截距:'+ str(mdl.intercept_))
print( '均方误差:'+str(((y-sim_y)*(y-sim_y)).sum()))
print( '损失函数loss值:'+str(((y-sim_y)*(y-sim_y)).sum()/(2*x.shape[0])+alpha*(abs(mdl.coef_.sum()))))
print('迭代次数:'+str(mdl.n_iter_))运行结果如下:
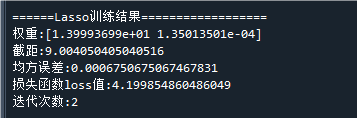
代入模型表达式,可得到模型为:
可以看到,第二个变量的系数已接近于0,说明第二个变量在模型中是可去除的
这就是Lasso回归的好处,在X1,X2线性相关时,其中一个变量的系数会趋于0
如何自实现Lasso回归
如果想自实现Lasso回归,而不是调用函数,可参考《Lasso回归-原理与自实现》
它详细介绍了sklearn内部如何实现Lasso回归的,并复现一模一样的效果
好了,以上就是Lasso回归模型的介绍与使用方法了~
End
 评论
评论