
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
AdaBoost自适应Boosting是一种经典的用于二分类的Boosting集成算法
本文讲解AdaBoost的模型结构,算法原理以及训练过程,并展示一个AdaBoost使用例子
通过本文可以快速了解AdaBoost是什么,有什么用,以及如何使用AdaBoost解决二分类问题
本节讲解AdaBoost的模型表达式以及损失函数,快速了解AdaBoost是什么
AdaBoost算法是什么
什么是AdaBoost集成算法
AdaBoost(Adaptive boosting)是一种基于Boosting,专为二分类问题设计的集成算法
Boosting集成,简单来说就是逐个训练弱模型,通过不断增加弱模型来逐步提升整体模型效果
AdaBoost以Boosting方式集成多个弱二分类模型来产生泛化能力好、预测精度高的强二分类模型
如下所示,AdaBoost集成多个决策进行决策:
Adaboost的模型表达式为:
其中,
: 第个决策器,输出必须是{-1,1}
: 决策器的权重系数,为正数
可以看到,Adaboost模型就是一系列决策器的加权和,即所有决策器的加权结果
AdaBoost的决策器与AdaBoost提升树
值得注意的是,虽然AdaBoost的决策器理论上的输出必须是{-1,1}
但实际中可以是任意二分类模型,因为只需把二分类模型的输出转换为{-1,1}就可以了
在实际使用中,AdaBoost一般以Cart分类树作为决策器,此时,则称为AdaBoost提升树
AdaBoost的损失函数
AdaBoost的损失函数
AdaBoost的损失函数为指数损失函数,如下:
其中, :样本个数
:模型对第i个样本的预测值
即
AdaBoost单个决策器的损失函数
AdaBoost在训练第k个决策器时,则使用下述损失函数
AdaBoost第k个决策器的损失函数:
其中, :样本个数
:前k个决策器对第i个样本的预测值
即
本节讲解AdaBoost算法是如何训练的,以及AdaBoost的算法流程
Adaboost的训练算法-流程
Adaboost的训练方法
Adaboost采用前向分步算法训练,即在已有决策器的基础上逐个添加新的决策器
每个决策器都力求损失函数最小化,直到新增决策器无法降低损失函数则停止训练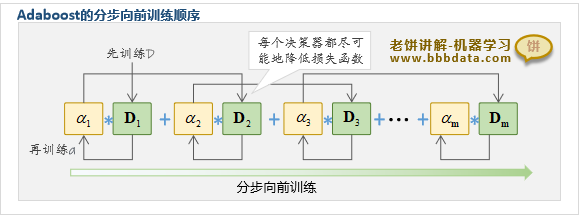
值得注意的是,Adaboost在训练第k个决策器 时
决策器 和系数 是拆开分别训练的,先训练 ,后训练 系数
一、决策器的训练
每个决策器以不同的样本权重来训练
第1个决策器的样本权重为:
,N为样本个数
第k个决策器的样本权重为:
二、决策器系数的训练
第k个决策器系数的计算公式如下:
其中,
直观地理解,Adaboost就是通过修改样本权重使每次的决策器偏向上一个决策器的错误样本
在训练第k个决策器时,把第k-1个决策器预测错误的样本权重调大,预测正确的样本权重调小
Adaboost的算法流程
Adaboost的具体算法流程如下:
Adaboost训练算法-原理
下面进一步解说,AdaBoost训练中相关公式的原理
决策器Dk的样本权重更新公式-原理解说
Adaboost的原始目的是令新增的每个决策都能使损失函数进一步最小化,即最小化
第k个决策器损失函数化简后得到
如果直接使用上述损失函数来训练模型的第k个决策器,这会改变决策器原有的训练方式
因此AdaBoost不妨将第i个样本的权重修改为,让决策器按原有方式训练
这是因为仔细观察可以发现,其实就是所有错误样本以为权重的加权和
所以修改样本权重让决策器按原方式训练,虽不能等同于最小化,但仍可起到类似效果
进一步地,对样本权重进行化简,就可得到样本权重迭代公式:
决策器系数αk的计算公式-原理解说
决策器系数的求解原理较为简单,只需要求解在损失函数中的驻点即可
即由可得
其中,
本节展示一个AdaBoost的实现例子,具体使用AdaBoost解决二分类问题
AdaBoost应用例子与代码
下面以Cart决策树作为AdaBoost的决策器,展示如何实现一个AdaBoost提升树
具体代码示例如下:
# -*- coding: utf-8 -*-
"""
本代码展示一个调用sklearn包实现Adaboost提升树算法的Demo
本代码来自《老饼讲解-机器学习》www.bbbdata.com
"""
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles
# --------------- 数据生成 -------------------
# 生成2维正态分布,生成的数据按分位数分为两类,500个样本,2个样本特征,协方差系数为2
X, y = make_gaussian_quantiles(cov=2.0,n_samples=500, n_features=2,n_classes=2, random_state=1) # 生成训练样本数据
# --------------- 模型训练与预测 -------------------
base_clf = DecisionTreeClassifier(max_depth=2, min_samples_split=20, min_samples_leaf=5) # 初始化决策树作为决策器
clf = AdaBoostClassifier(base_clf,algorithm="SAMME",n_estimators=50, learning_rate=0.8) # 初始化AdaBoost
clf.fit(X, y) # 模型训练
pred = clf.predict(X) # 模型预测的类别
proba = clf.predict_proba(X) # 模型预测的概率
# ----------------- 打印结果-------------------------
fig, axes = plt.subplots(2, 1,figsize=(10, 6)) # 初始化画布
plt.subplots_adjust(wspace=0.2, hspace=0.3) # 调整画布子图间隔
axes[0].scatter(X[:, 0], X[:, 1], c=y) # 画出样本与真实类别
axes[0].set_title('sample-true-class') # 设置第一个子图的标题
axes[1].scatter(X[:, 0], X[:, 1], c=pred) # 画出样本与预测类别
axes[1].set_title('sample-predict-class') # 设置第二个子图的标题
plt.show() # 显示画布
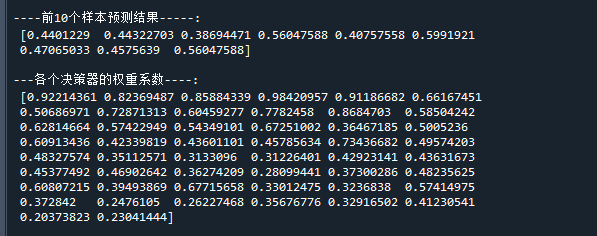
print("\n----前10个样本预测结果-----:\n",proba[1:10,1]) # 打印前10个样本的预测值
print("\n---各个决策器的权重系数----:\n",clf.estimator_weights_) # 打印决策器权重运行结果如下:
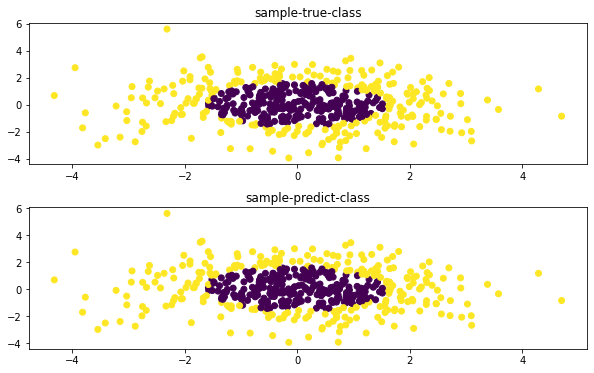
从图中可以看到,模型的预测类别与真实类别几乎是一致的
老饼语
与随机森林这些算法一样,AdaBoost随着Xgboost的出现,渐渐退出了舞台
但由于历史原因,在机器学习中各类模型,AdaBoost还是一个知名度较高的模型
本文作为AdaBoost算法的入门文章,主要介绍它是什么、怎么用所以在一些原理细节上能省就省
如果需要了解具体的细节,可以参考《课程:AdaBoost-原理与自实现》
在课程中自写代码实现AdaBoost,结果与sklearn一致,因为它就是笔者阅读sklearn源码而整理出来的代码
在课程中对AdaBoost实现时所所涉及的原理都进行详细讲解,并提供各个公式的详细推导
好了,以上就是AdaBoost集成算法的介绍了~
End
 评论
评论