
本站原创文章,转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
RBF神经网络是Powell在1985年提出的一种基于RBF函数的神经网络,它用于解决回归问题
本文讲解RBF神经网络的思想、模型结构、训练方法,以及径向基神经网络的代码实现
通过本文可以快速了解什么是RBF神经网络,以及如何使用RBF神经网络来解决数值预测问题
本节讲解RBF神经网络的思想与原理,快速了解RBF神经网络是什么
RBF函数是什么
RBF神经网络以RBF函数为基础,下面我们先介绍什么是RBF函数
RBF(Radial Basis Function)函数又称为径向基函数,它是指如下形态为钟形的函数
例如高斯函数或者就是一个最经常见到的RBF函数
径向基函数的特色就是局部性,即只有中心部分非0,其它部分近似于0,离中心越远越近似于0
什么是RBF神经网络
RBF神经网络是一种以RBF为激活函数的神经网络,可用于回归问题,即数值预测
RBF神经网络解决回归问题的思路如下:
由于RBF函数只对其中心部分有较大影响,而不怎么影响其它地方
因此,RBF神经网络利用RFB函数的这种局部性,在每个局部都用一个RBF去拟合目标
最终凑合多个RBF函数,就可得到一条可以拟合全局所有样本数据点的平滑曲线
如图所示,RBF神经网络以各个样本数据点为中心,来生成多个RFB径向基曲线
然后通过叠加所有RBF曲线,就可得到一条能够光滑拟合各个样本数据点的曲线
总的来说,RBF神经网络的原理就是每个局部都用一个RBF函数去拟合,最终达到全局拟合
本节讲解RBF神经网络的拓扑结构和模型表达式
RBF神经网络的结构拓扑
RBF神经网络的拓扑结构
RBF神经网络一般用三层的神经网络来表示,它的拓扑结构如下:
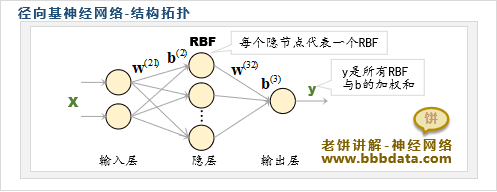
RBF神经网络模型的数学表达式如下:
其中
:径向基函数,一般取为
:距离函数,一般取为欧氏距离函数
✍️RBF神经网络结构解说
紧扣RBF神经网络就是多个RBF函数之和来理解RBF神经网络的拓扑图,如下:
隐层每个隐节点都代表一个RBF,有多少个RBF就有多少个隐节点
其中,输入层到隐层的权重代表RBF的中心,隐层阈值代表RBF的宽度
是矩阵,它的第i行是第i个RBF的中心,是向量,第i个元素代表第i个RBF的宽
最后,各个RBF用进行加权求和,并加上阈值,就是RBF神经网络最终的输出
是第i个RBF在第j个输出中的权重,也可以认为它是第i个RBF在第j个输出中的高
RBF神经网络结构-示例解说
以一个2输入、3个隐节点、1个输出的RBF神经网络为例
它的拓扑结构如下:
数学表达式如下:
进一步地
把RBF取为高斯函数,dist取为欧氏距离,则有:
可以看到,RBF神经网络的输出就是多个RBF的叠加结果
本节介绍径向基神经网络的求解方法
RBF神经网络的训练方法
RBF神经网络的训练就是求解w和b,使得最终模型的输出与真实y值一致
径向基神经网络的常见基本训练方法有三种,如下:
👉 1. 插值求解 :matlab的工具箱中的newrbe函数
👉 2. OLS求解法 :matlab的工具箱中的newrb函数
👉 3. K-means聚类法 :matlab不提供该方法
RBF神经网络的插值求解方法
使用插值求解时,RBF神经网络在训练数据上的预测误差为0
RBF的插值求解方法如下:
1. 先预设径向基的宽度,即是预设值
2. 以每个样本为中心,即以历史样本X作为
可知,如果有n个样本,那么就会生成n个隐节点径向基
3. 精确求解
由于与已经确定,所以各个RBF隐节点的值h就是一个确定值
通过解以下方程,即可得到RBF神经网络输出层的权重与阈值:
由于h是n维方阵,故方程必可解,即预测值与真实值一致,模型误差为0
插值求解的优点是训练误差为0,而缺点是有n个样本就有n个径向基,模型会非常庞大
RBF神经网络的OLS求解方法
OLS求解法(正交最小二乘法)是对精解求解法的一种优化,它的目的是减少RBF的个数
OLS先以n个样本生成n个径向基,再将径向基逐个添加到模型,直到模型误差足够小

如图所示,使用OLS求解时,随着径向基的添加,模型的误差在逐步下降
一般在实际使用中,我们先将目标误差设为0,打印出RBF神经网络误差下降的整个过程
然后再选择一个合适的误差重新训练,使得模型既能满足误差要求,又能使隐节点尽量的少
本节实现一个RBF神经网络,用于拟合历史样本数据
RBF神经网络-代码实现
下面使用matlab的newrb函数,实现一个RBF神经网络拟合历史样本数据
具体代码实现如下:
%代码说明:径向基newrb的matlab工具箱使用Demo
%来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2018a
%-----------------------------------------------------
%----数据准备----
close all
x = [-2 -1 0 1 2];
y = [3 2 3 1 2]; % 输出数据
%----网络训练----
[net,tr] = newrb(x, y, 0.01, 0.5); % 以X,Y建立径向基网络,目标误差为0.01,径向基的宽度参数spread=0.5
simY = sim(net,x) % 用建好的网络拟合原始数据
perf = tr.perf
w21 = net.iw{1}
b2 = net.b{1}
w32 = net.lw{2,1}
b3 = net.b{2}
%----绘制拟合曲线----
figure(1);
hold on
t = -2:0.1:2;
rbf = repmat(w32',1,size(t,2)).* exp(-(repmat(b2,1,size(t,2)).*dist(w21,t)).^2);
simt = sum(rbf) + b3;
for i = 1:size(rbf,1)
plot(t,rbf(i,:),':')
end
plot(x,y,'*')
plot(t,simt,'r') 代码运行结果如下:
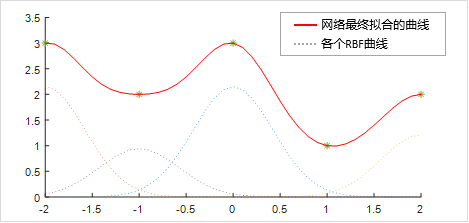
在程序中我们设置了误差目标为0.01,当添加了4个隐节点时,误差就已经满足要求
备注:perf的第一个0.56,代表的是没有添加任何隐节点时模型的误差
从拟合结果中可以看到,训练好的RBF神经网络已经完美地拟合了所有历史样本数据点
老饼编后语
本篇文章主要为了希望能简单、快速了解RBF神经网络的同学而准备
但要更具体、详细地了解RBF神经网络,请看RBF的专栏文章《RBF神经网络-入门》
在栏目里再详细讲解RBF神经网络的原理是什么、它的参数意义,以及建模流程和案例
过多的细节需要更多的耐心,因此,本文仅仅是为了快速地了解、使用RBF而写,祝大家学习顺利~
好了,以上就是RBF神经网络的入门介绍了~
End
 评论
评论