
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
梯度下降法是训练MLP神经网络的基本算法,在数据较小时,可以直接使用梯度下降法进行训练
本文讲解什么是梯度下降法,以及梯度下降法训练MLP的算法流程,并展示具体的实现代码与训练结果
通过本文,可以了解梯度下降法是什么,如何用梯度下降法训练MLP,以及它的代码实现方法
本节介绍梯度下降算法,以及如何使用它来训练MLP神经网络
梯度下降算法-简介
梯度下降算法是机器学习的优化算法中最基础的一种算法
例如要求一使尽量的小,梯度下降算法的思路如下:
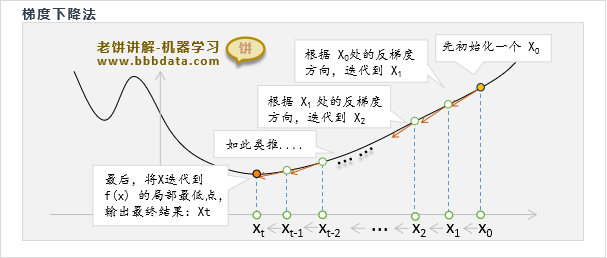
梯度下降算法先取一个初始值,然后进行迭代,每次都往梯度的反方向调整它
直到满足迭代条件(例如无法令目标函数值下降,或达到到最大迭代次数),则退出训练
梯度下降法的更多介绍可以参考文章《梯度下降算法》
梯度下降法训练MLP-算法流程
梯度下降算法求解MLP神经网络的流程如下:
一、先初始化w,b
简单地,可以采用随机初始化即可
二、迭代
1. 计算所有w,b在当前处的梯度gw,gb
2. 将w,b往负梯度方向更新:
w = w-lr*gw
b = b-lr*gb
这里的lr是预设的学习率,例如设为0.1
3. 判断是否满足退出条件,如果满足,则退出迭代
总的来说,使用梯度下降算法训练MLP神经网络时,
只需要初始化一个解,然后将解不断往损失函数的负梯度方向调整就行
本节展示一个用MLP解决数值预测的例子,以及具体代码实现
梯度下降法训练MLP-代码示例
如下所示,在sin函数[-5,5]之间采集20个数据,我们需要训练一个三层MLP神经网络,来拟合sin函数x与y的关系
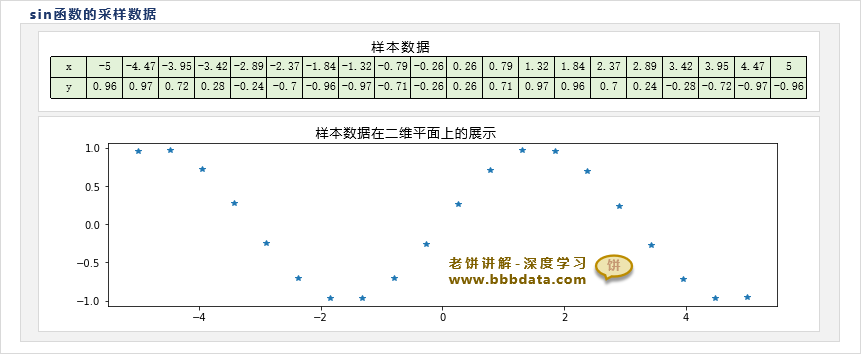
由于样本较为简单,我们不妨将三层MLP神经网络设为4个隐节点,并使用均方差作为损失函数
根据梯度下降算法的流程,对三层MLP进行训练,具体代码实现如下:
import torch
import matplotlib.pyplot as plt
torch.manual_seed(99)
# -----计算网络输出:前馈式计算------
def forward(w1,b1,w2,b2,x):
return w2@torch.tanh(w1@x+b1)+b2
# -----计算损失函数: 使用均方差------
def loss(y,py):
return ((y-py)**2).mean()
# -----训练数据----------------------
x = torch.linspace(-5,5,20).reshape(1,20) # 在[-5,5]之间生成20个数作为x
y = torch.sin(x) # 模型的输出值y
#-----------训练模型-----------------
in_num = x.shape[0] # 输入个数
out_num = y.shape[0] # 输出个数
hn = 4 # 隐节点个数
w1 = torch.randn([hn,in_num],requires_grad=True) # 初始化输入层到隐层的权重w1
b1 = torch.randn([hn,1],requires_grad=True) # 初始化隐层的阈值b1
w2 = torch.randn([out_num,hn],requires_grad=True) # 初始化隐层到输出层的权重w2
b2 = torch.randn([out_num,1],requires_grad=True) # 初始化输出层的阈值b2
lr = 0.01 # 学习率
for i in range(5000): # 训练5000步
py = forward(w1,b1,w2,b2,x) # 计算网络的输出
L = loss(y,py) # 计算损失函数
print('第',str(i),'轮:',L) # 打印当前损失函数值
L.backward() # 用损失函数更新模型参数的梯度
w1.data=w1.data-w1.grad*lr # 更新模型系数w1
b1.data=b1.data-b1.grad*lr # 更新模型系数b1
w2.data=w2.data-w2.grad*lr # 更新模型系数w2
b2.data=b2.data-b2.grad*lr # 更新模型系数b2
w1.grad.zero_() # 清空w1梯度,以便下次backward
b1.grad.zero_() # 清空b1梯度,以便下次backward
w2.grad.zero_() # 清空w2梯度,以便下次backward
b2.grad.zero_() # 清空b2梯度,以便下次backward
if(L.item()<0.005): # 如果误差达到要求
break # 退出训练
px = torch.linspace(-5,5,100).reshape(1,100) # 测试数据,用于绘制网络的拟合曲线
py = forward(w1,b1,w2,b2,px).detach().numpy() # 网络的预测值
plt.scatter(x, y) # 绘制样本
plt.plot(px[0,:],py[0,:]) # 绘制拟合曲线
plt.show() # 展示画布
print('w1:',w1) # 打印w1
print('b1:',b1) # 打印b1
print('w2:',w2) # 打印w2
print('b2:',b2) # 打印b2运行结果如下:

可以看到,模型根据训练数据,已经较好地拟合出sin函数曲线
将模型参数代回MLP神经网络的数学表达式,即可得到模型的数学表达式为:
好了,以上就是梯度下降算法训练MLP神经网络的方法与具体代码例子了~
End
 评论
评论