
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
决策树模型(Decision Tree)是机器学习中最常用的模型之一,它可用于分类,也可用于回归
本文讲解决策树是什么,以及CART决策树的原理、构建流程、剪枝方法,并展示具体的实现例子
通过本文,可以快速了解什么是决策树模型,什么是CART决策树以及如何具体地使用CART决策树
本节介绍有哪些决策树,各种决策树分别是什么
决策树模型是什么
决策树模型(Decision Tree)是机器学习中最常用的模型之一
决策树模型共有三类,如下:
👉1. ID3决策树
👉2. C4.5决策树
👉3. CART决策树
三种决策树模型都是分类模型,用于预测样本的类别,但CART也可以用于回归(预测数值)
ID3是最早的决策树,由昆兰1979年提出,然后再有C4.5,最后才是CART决策树
但目前日常一般使用的都是CART决策树,像matlab、sklearn等都只提供CART决策树模型
ID3、C4.5与CART决策树-介绍
ID3决策树
ID3决策树是最早提出的决策树模型,ID3是一棵全分裂树,它只支持枚举变量,如下:
ID3决策树在构建时,每次选择其中一个变量,然后将所有取值各作为一个分枝子节点
直到节点上的样本不再值得分枝时(例如样本的类别都一样)就作为叶子节点,标上类别
在使用决策树模型时,只需跟随根节点逐步决策,最后到达的叶子节点就是样本的类别
C4.5决策树
C4.5决策树主要是解决ID3决策树的一些缺点,以及支持连续变量,C4.5决策树如下:
可以看到,决策树C4.5算法不仅支持枚举变量,也支持连续变量,使模型兼容性更强
当节点上是连续变量时,C4.5选择一个阈值将样本一分为二,并生成两个分枝子节点
除了支持连续变量,C4.5算法在训练时还引入相关机制,解决了ID3的其它3个缺点:
(1)ID3偏好多枚举值变量、(2)ID3易过拟合 、(3)ID3不支持数据有缺失值
CART决策树
CART(Classification And Regression Tree)全称为分类与回归树,可用于分类和回归
CART决策树模型是目前使用最多的一种决策树,它是一棵二叉树,且只支持数值变量
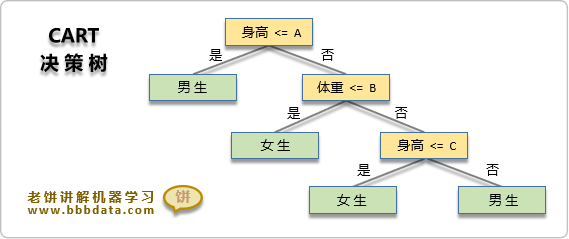
CART决策树在构建时,每次选择一个变量与切割点将样本一分为二,得到左右两个节点
左节点与右节点作为子节点继续各自生长、分裂,直到满足条件则停止生长,完成构建
备注:CART决策树的变量是可重复选择的
✍️不同决策树之间的关系
1. ID3可以看作是一个初代版本,可用但仍有很多问题
2. C4.5则是ID3的加强版,它对ID3的相关严重问题都进行了补充与改进
3. CART则是C4.5的精华版本,去掉了C4.5一些不必要的功能,是目前一般使用的版本
虽然C4.5看起来是最强大的,但它对ID3的许多改进未必是可取的,例如缺失值的处理就极为复杂与臃肿
CART虽然看起来没C4.5强大,但其实是去其糟粕,取其精华后的结果,因此实际使用中更多用的是CART
总的来说,决策树在优化改善上走了很漫长的一段路,最后生下的娃就是CART决策树,简洁、精巧、专业
本节讲解决策树模型的几何意义,更加形象理解决策树模型
决策树模型的几何意义
由于决策树最终就是由叶子节点所落在的范围,来决定样本的类别,
所以决策树的本质就是对X进行分段、分块,再根据样本所在段块来判别类别,如下:
✍️回归树的本质
特别地,当决策树用于回归时,则可以将决策树理解为一个分段函数:
而回归树正是通过不断切割X、细化X,并令每一段取其均值,从而迫近目标函数
本节讲解Cart决策树模型的构建,以及几何意义
CART决策树的构建
决策树构建的目标就是构建出一棵树,使得历史样本在决策树上分类尽量准确
整个构建的理念是通过不断分枝,使历史样本的类别信息更加明确
CART决策树模型的构建过程如下:
1. 初始化一个根节点
2. 对非叶子节点进行分枝:
对非叶子节点选择一个变量与一个分割值,将样本一分为二,得到左右两个节点
并判断左右两个节点是否满足成为叶子节点的条件,如果满足,则标上节点的预测值
3. 重复2,直到所有节点都成为叶子节点
其中两个细节如下:
1. 分裂时如何选择变量与分割值:
历遍所有的【变量-分割值】组合,哪种分割最优,就选择哪种【变量-分割值】
分类树判断【变量-分割值】的分割质量时的评估函数为: 基尼函数,信息增益(熵)函数
回归树判断【变量-分割值】的分割质量时的评估函数为: 平方差函数
2. 叶子节点的预测值如何确定:
对于分类树:叶子节点上的样本,哪个类别最多,就作为叶子节点的预测类别
对于回归树:取叶子节点上样本y值的平均值,作为叶子节点的预测值
CART决策树节点分枝的评估函数
CART决策树用于评估【变量-分割值】的分裂质量时,所使用的函数为:
👉1. Gini基尼函数 :用于分类树
👉2. Gain熵函数 :用于分类树,也称为信息增益函数
👉3. 平方差函数 :用于回归树
下面我们详细介绍这三个函数的表达式
Gini基尼函数
GINI函数代表分裂后,在左(或右)节点随机抽取两个样本,它们类别不同的概率
Gini函数的表达式如下:
其中
: 划到左节点的样本个数
: 划到右节点的样本个数
: 本次划分的总样本个数,即
: 左节点上属于 类的个数
: 右节点上属于 类的个数
Gini函数的意义与推导详见《决策树GINI系数的意义与推导》
信息增益(Gain)函数
信息增益函数的意义是分叉后比分叉前信息量(不确定性)的减少量
信息增益函数又称为熵函数,它的表达式如下:
其中
: 划到左节点的样本个数
: 划到右节点的样本个数
: 本次划分的总样本个数,即
: 属于 类的样本个数
: 左节点上属于 类的个数
: 右节点上属于 类的个数
CART决策树中的平方差函数
平方差函数用于CART回归树,它代表分叉后的预测误差
CART回归树中的平方差函数如下:
本节讲解CART决策树模型的预剪枝与后剪枝,以及CCP后剪枝的使用方法
CART决策树的剪枝
易知,只要CART决策树生长得足够深(即对X分割得足够细),它可以拟合所有样本
因此,CART决策树是一种较易出现过拟合的模型,一般地,决策树通过剪枝来预防过拟合
决策树的剪枝分为:预剪枝与后剪枝,它们可以有效减少决策树过度生长导致过拟合的问题
决策树的预剪枝
预剪枝是树构建过程,达到一定条件就停止生长,
在sklearn中,预剪枝实际就是调参,通过设置树的生长参数,来达到预剪枝的效果
决策树的后剪枝
后剪枝就是我们理解中的剪枝,即等树生长完后再对其剪枝,使决策树模型更加简单
决策树后剪枝一般使用的是CCP(Cost Complexity Pruning)代价复杂度剪枝算法
CCP后剪枝选择部分节点进行剪枝,它的目标是使以下损失函数最小化:
其中,:叶子节点个数
:所有样本个数
:第 i 个叶子节点上的样本数
:第i个叶子节点的损失函数
在sklearn中,criterion设为entropy时,Li是第i个叶子的熵
criterion设为GINI时,则是第i个叶子的GINI系数
:复杂度惩罚系数,用于惩罚节点个数
在CCP损失函数中,既考虑了代价,又考虑了树的复杂度,所以称为代价复杂度剪枝法
CCP剪枝的目的就是在树的复杂度与准确性之间取得一个平衡点,并用控制树复杂度的权重
CPP后剪枝的使用
CCP后剪枝在使用时,一般先打印CCP路径,然后根据CCP路径自主剪枝,具体如下:
一、打印CCP路径
CCP路径一般包含三个信息:
1. alpha 值
2. alpha 值对应剪掉的节点编号
3. 剪掉节点后树的Cost(代价,或者质量)
备注:代价的定义在各个软件不一定相同
在python的sklearn中,代价指的是所有叶子的GINI值/熵值
在matlab中,用的则是判断错误的样本占比
二、根据CCP路径自主剪枝
分析CPP路径,在节点与代价之间自主权衡,选择要裁剪的节点,进行剪枝
备注:剪枝的调用方式在不同软件中不一定相同
在python的sklearn中,后剪枝是通过设置alpha,重新训练决策树来达到剪枝
而matlab则是根据节点编号,直接调用剪枝接口对节点进行裁剪
本节展示CART决策树的实现例子,以及剪枝例子,进一步具体掌握CART决策树的应用
CART决策树例子-预测类别
下面以iris鸢尾花数据为例,展示如何实现一个CART决策树用于类别预测
iris鸢尾花数据如下:
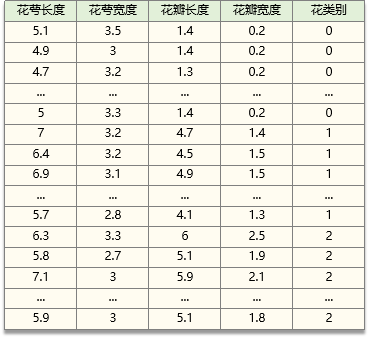
iris鸢尾花数据共包含4个变量,以及3个鸢尾花类别:
花萼长度 sepal length (cm) 、花萼宽度 sepal width (cm)
花瓣长度 petal length (cm) 、花瓣宽度 petal width (cm)
山鸢尾:0,杂色鸢尾:1,弗吉尼亚鸢尾:2
使用python的sklearn实现决策树的代码如下:
from sklearn.datasets import load_iris
from sklearn import tree
#----------------数据准备-----------------------
iris = load_iris() # 加载数据
clf = tree.DecisionTreeClassifier() # sk-learn的决策树模型
clf = clf.fit(iris.data, iris.target) # 用数据训练树模型
#---------------模型预测结果--------------------
test_x = iris.data[[0,1,50,51,100,101], :] # 用于预测的X
test_y = iris.target[[0,1,50,51,100,101]] # 用于预测的y
pred_target_prob = clf.predict_proba(test_x) # 预测类别概率
pred_target = clf.predict(test_x) # 预测类别
#---------------打印结果------------------------
print("\n===测试数据:===============\n",test_x) # 打印测试数据
print("\n===测试数据的真实类别:=====\n",test_y) # 打印测试数据的真实类别
print("\n===预测所属类别概率:=======\n",pred_target_prob) # 打印测试数据的预测概率
print("\n===预测所属类别:===========\n",pred_target) # 打印测试数据的预测类别运行结果如下:
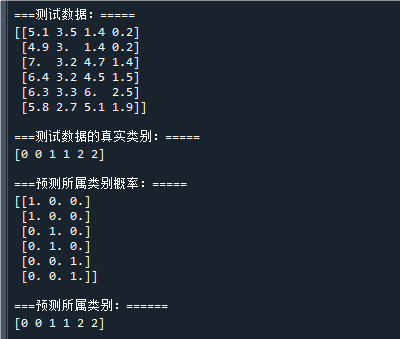
可以看到,模型的预测类别与真实类别一致,说明模型是有效的
CART决策树例子-剪枝示例
CART决策树分为预剪枝与后剪枝,
预剪枝就是在训练时设定相关参数,使决策树不要过度生长
后剪枝则采用CCP后剪枝,打先印CCP路径,再选择性进行剪枝
决策树剪枝的具体代码示例如下:
# -*- coding: utf-8 -*-
from sklearn.datasets import load_iris
from sklearn import tree
import numpy as np
#----------------数据准备----------------------------
iris = load_iris() # 加载数据
X = iris.data # 用于训练的X
y = iris.target # 用于训练的y
#---------------模型训练---------------------------------
clf = tree.DecisionTreeClassifier(min_samples_split=10,ccp_alpha=0) # 初始化决策树模型,这里设置min_samples_split就是一种预剪枝策略
clf = clf.fit(X, y) # 训练决策树
pruning_path = clf.cost_complexity_pruning_path(X, y) # 计算CCP路径
#-------打印结果---------------------------
print("\n====CCP路径=================") # 打印CCP路径
print("ccp_alphas:",pruning_path['ccp_alphas']) # 打印CCP路径中的alpha
print("impurities:",pruning_path['impurities']) # 打印CCP路径alpha对应的不纯度运行结果如下:
它的意思是:
时,树的不纯度为 0.02666
时,树的不纯度为 0.03082
时,树的不纯度为 0.04387
........
这里的不纯度是CCP损失函数中的,即所有叶子的不纯度(gini或者熵)加权和
进一步地,根据决策树的质量(不纯度),选择合适的alpha重新训练决策树,就完成了后剪枝
笔者语
决策树虽然是一个简单的模型,但内容实在太多了,本文仅尽量满足入门所需
如何深入应用决策树
日常的使用可以参考本站决策树系列文章《决策树-专题详述》,
该系列文章囊括决策树模型日常的应用,包括决策树的参数讲解、决策树可视化、建模流程等等
如何深入决策树的原理
如果不想调用软件包,而是自行实现一个决策树,可参考课程《课程:Cart决策树-原理与自实现》
该课程是老饼阅读matlab的决策树源码后整理出来的课程
在课程中讲解决策树相关的细节原理,并用python复现出与matlab决策树函数一模一样的结果
好了,以上就是决策树的介绍,以及CART决策树的原理与应用了~
End
 评论
评论