
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
Adam算法(Adaptive Moment Estimation)是目前深度学习中最常用的一种优化算法
它没有太多新内容,只是简单地整合了RMProp算法与动量梯度下降法,从而得到的一种效果更佳的优化算法
本文讲解Adam算法的计算公式,并对公式逐行解读,以及展示Adam算法的一个简单代码实现例子
本节介绍Adam算法的算法流程
Adam算法是什么
Adam算法的更新公式
Adam算法(Adaptive Moment Estimation)是目前深度学习中最常用的一种优化算法
它没有太多新内容,只是简单地整合了RMProp算法与动量梯度下降法,从而得到的一种效果更佳的优化算法
因此,Adam算法的特点就是,既拥有RMProp的自适应学习率,同时又能像动量法那样,跳出局部最优
记待优化的第i个参数为,Adam算法的更新公式如下:
(1)
(2)
(3)
(4)
(5)
其中,:参数的梯度
:的速度,初始值为0
:的累计平方和,初始值为0
:的衰减系数,取值范围为[0,1],一般设为0.9
:的衰减系数,取值范围为[0,1],一般设为0.999
:当前的迭代次数
:学习率
:一个极小的常数,它的作用避免分母为0
Adam算法公式解读
参考RMProp算法与动量梯度下降法就能理解Adam算法了
(1)式参考动量梯度下降法,它引入速度来作为更新时的迭代量
(2)式参考RMProp算法,引入累计平方和来自适应地调整学习率
(3),(4)式则是对v、s的修正
主要是在迭代初期,v、s会偏小,因此对它们进行修正
当迭代次数达到一定次数后,会近似于0,此时就近似于了
(5)式用于更新参数x
它参考RMProp算法,使用来调整学习率
同时参考动量梯度法,用来替代梯度作为迭代量
总的来说,Adam算法就是引入了动量法中的速度作为更新量、并采用了RMProp中的自适应学习率
并加上了一点小技巧,对v、s作了一点小修正(事实上修不修正都没多大关系,毕竟影响的只有前面的几次迭代)
本节展示Adam算法的具体代码实现
Adam算法-代码实现
下面使用Adam算法来求函数的最小值
由于Adam算法需要使用目标函数的梯度,所以需要先算出梯度,如下:
,
Adam算法的具体实现代码如下:
"""
Adam算法求y= (x1-2)^2+(x2-3)^2的最小解
"""
import numpy as np
x = np.array([0,0]) # 初始化x
lr = 0.01 # 设置学习率
beta1 = 0.9 # 设置beta1
beta2 = 0.9 # 设置beta2
s = np.array([0,0]) # 初始化梯度累计量
v = np.array([0,0]) # 初始化速度
esp = 0.000001 # 很小的常数
for i in range(1000): # 最大迭代1000次
g = np.array([2*x[0]-4, 2*x[1]-6]) # 计算x的梯度
v = beta1*v + (1-beta1)*g # 更新速度
s = beta2*s + (1-beta2)*g*g # 更新梯度累计量
vc = v/(1-beta1**(i+1)) # 修正速度
sc = s/(1-beta2**(i+1)) # 修正梯度累计量
x = x - lr/(np.sqrt(sc)+esp)*vc # 调整x
print("第",i+1,"轮迭代:x=[",x[0],",",x[1],"],y=",(x[0]-2)**2+(x[1]-3)**2) # 打印当前结果
if((max(abs(g))< 0.001) ):break # 如果梯度过小,则退出迭代运行结果如下:
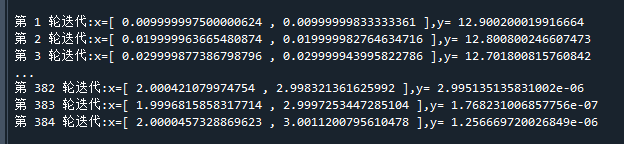
可以看到,经过了384轮迭代,所得到解已经非常接近真实极小解[2,3]
好了,以上就是Adam算法的简单介绍了~
End
 评论
评论