
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
蚁群算法(Ant Colony Optimization, ACO)是一种模拟蚂蚁觅食行为的智能优化算法
本文讲解蚁群算法的思想、原理,以及具体的算法流程,并展示算法流程图
通过本文,可以快速了解蚁群算法是什么,有什么用,以及蚁群算法的详细算法流程
本节讲解蚁群算法的思想与原理,初步了解蚁群算法是什么
蚁群算法ACO是什么
蚁群算法(Ant Colony Optimization, ACO)是1992年由Marco Dorigo提出的一种优化算法
它的原理主要模拟蚂蚁觅食行为,在蚁群觅食时,蚁群总是能找到一条较短的路径来搬运食物
这是因为在觅食过程中,每个蚂蚁都会在路径上留下信息素来共享信息,越好的路径,留下的信息素越多
而在蚂蚁路径选择时,会偏向于信息素越多的路径,这样,经过一段时间后,整体就会趋向更优秀的路径
蚁群算法可以说是为TSP问题量身打造的算法,可以紧扣TSP问题来理解蚁群算法
TSP问题就是要找出一条距离最小的路径,因此如何选择下一个节点就是TSP问题的核心
蚁群算法引入了信息素,在城市选择下一个城市时,每个可选城市的评估函数如下:
其中,和 分别是从i城市到j城市的信息素和距离 ,则是预设的权重因子
从公式可以看到,它既考虑当前节点到达下一个节点的距离,又考虑了历史蚂蚁遗留的信息素
在这里,"距离"可以理解为待选节点在当前局部的优势,而"信息素"则代表着节点的全局优势
因此,蚁群算法通过多次迭代,使得信息素对于全局的评估越来越准确,从而最终引导蚂蚁走上更优的路径
总的来说,蚁群算法就是借鉴了蚂蚁会遗留信息素来分享全局信息的特点,用于解决TSP问题的一种智能优化算法
本节介绍蚁群算法的算法流程,以及算法流程图
蚁群算法-算法流程
蚁群算法的算法流程图如下:
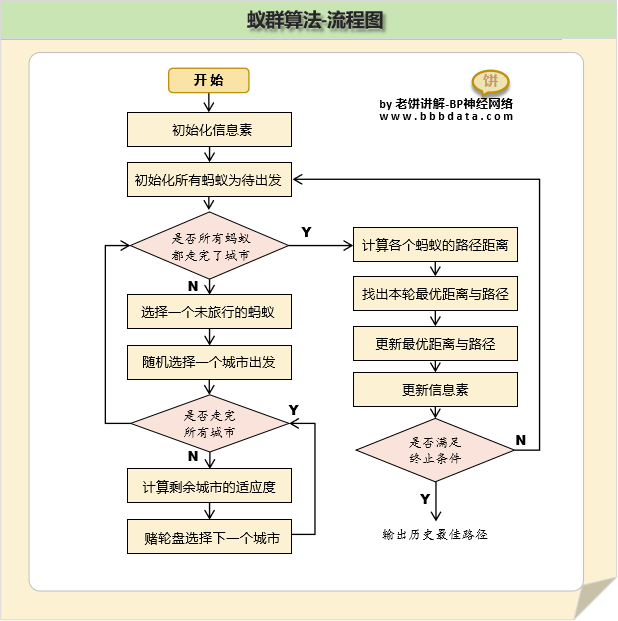
蚁群算法的详细算法流程如下:
一、初始化
1. 初始化每条路径的信息素
设 为第i个城市到第j个城市的信息素,将它初始化为1
2. 初始化最优路径、最优距离
二、循环迭代
1. 逐个蚂蚁循环,计算每个蚂蚁所走路径
当前蚂蚁先随机选择一个出发城市,然后依次选择剩余城市
(1) 计算剩余城市的选择概率
设当前所在城市为,则转移到j城市的适应度为:
其中, :信息素重要因子,可设为0.1
:启发函数重要因子,可设为10
:第i个城市到第j个城市的信息素
:第i个城市到第j个城市的距离
(2) 以赌轮盘的方式选择一个城市作为下一个城市
将的占比作为第j个城市在轮盘上的面积
随机转动轮盘,指针指向哪个城市,就选择哪个城市
重复(1),(2)步骤,直到该蚂蚁走完所有城市
2. 计算各个蚂蚁所走路径的距离d
不妨记第个蚂蚁所走路径的距离为
3. 找出本轮最优距离,以其对应的路径
4. 更新历史最优距离、最优路径
如果本轮最优距离小于历史最优距离
则更新:
5. 更新信息素
(1) 对所有边的信息素进行信息衰减
其中,:信息素衰减系数,可设为0.1
(2) 给每个蚂蚁所走路径的每条边添加1/d的信息素
(3) 给历史最优路径的每条边添加的信息素
这称为精英蚂蚁策略,可加速算法收敛
6. 检查终止条件
如果满足终止条件,则退出迭代,终止条件可设如下:
(1) 达到最大迭代次数
(2) 近n次历史最优距离没有明显下降
三、输出结果
1. 输出历史最优路径
2. 输出历史最优路径的距离
本节展示蚁群算法求解TSP问题的代码实现
蚁群算法求解TSP问题-代码实现
根据上述思路与蚁群算法算法流程,
用蚁群算法求解TSP问题的代码实现如下:
%------代码说明:展示蚁群算法求解TSP问题 -----------------
% 来自《老饼讲解神经网络》www.bbbdata.com ,matlab版本:2018a
clc;clear all;close all ;
rng(888) % 为方便复现结果,设定随机种子
cityLoc = [3.64,2.68; ... % beijing
4.18,1.76 ; ... % shanghai
3.71,2.60 ; ... % tianjin
1.33,3.30 ; ... % wulumuqi
4.20,2.96 ; ... % shenyang
3.92,1.82 ; ... % nanjing
2.55,1.64 ; ... % chengdu
2.37,1.02 ; ... % kunming
3.43,2.09 ; ... % zhengzhou
3.54,0.70 ; ... % xianggang
3.51,1.62 ; ... % wuhan
3.44,0.80 ; ... % guangzhou
3.24,2.77 ; ... % huhehaote
2.38,2.32 ; ... % xiling
2.56,2.24 ; ... % lanzhou
3.01,2.03 ; ... % xian
2.79,2.51 ; ... % yinchuan
4.03,1.16 ; ... % fuzhou
3.47,0.70 ; ... % aomen
1.30,1.69] ; % lasha
distMat = dist(cityLoc') ; % 计算城市距离
N = size(cityLoc,1); % 城市个数
%------参数设置与初始化------
m = 30; % 种群规模
T = 500; % 迭代次数
alpha = 1; % 信息素重要因子
beta = 5; % 启发函数重要因子
rho = 0.1; % 信息素衰减系数
tauMat = ones(N,N); % 信息素矩阵
dbest = inf; % 最优距离
xbest = []; % 最优路径
last_d = -inf(1,10); % 初始化最近10次的最佳结果
delta_goal = 0.001; % 近n次下降误差阈值
% ------迭代--------------
for t =1:T
% 计算蚂蚁路径
x = zeros(m,N); % 初始化各个蚂蚁的路径
for i = 1:m % 逐个蚂蚁循环
rest_city = 1:N; % 剩余的城市
x(i,1) = randi(N); % 随机选择第一个城市
rest_city(rest_city==x(i,1))=[]; % 将选择的城市从剩余城市移除
for j = 2:N % 逐个城市进行选择
last_city = x(i,j-1); % 上一次选择的城市
A = tauMat(last_city,rest_city).^alpha.*(1./distMat(last_city,rest_city)).^beta; % 计算各个城市的适应度
Psum = cumsum(A/sum(A)); % 生成轮盘
r = rand(); % 生成随机数
idx = min(find(r<Psum)); % 找出随机数指向轮盘的位置
select_city = rest_city(idx); % 本轮选择的城市
x(i,j) = select_city; % 保存本轮选择的城市
rest_city(rest_city==select_city)=[]; % 将选择的城市从剩余城市移除
end % -
end % -
% 计算每条路径的距离
xx = [x,x(:,1)]; % 拼上第一个城市,作为最后返回的城市
d = zeros(m,1) ; % 初始化每只蚂蚁的路径的距离
for i = 1:m % 逐个蚂蚁循环
for j = 1:N % 逐个城市循环
d(i) = d(i) + distMat(xx(i,j),xx(i,j+1)); % 累加当前城市的距离
end
end
% 打出最优路径
[dmin,idx_min] = min(d); % 本轮最小的距离
if(dmin<dbest) % 如果本轮结果优于历史结果
dbest = dmin; % 更新历史最优距离
xbest = x(idx_min,:); % 更新历史最优路径
end % -
% 更新信息素
tauMat = tauMat*(1-rho); % 信息素衰减
xx = [xx;[xbest,xbest(1)]]; % 拼上蚂蚁精英的路径
for i = 1:m % 逐个蚂蚁循环
for j = 1:N % 逐个城市循环
tauMat(xx(i,j),xx(i,j+1)) = tauMat(xx(i,j),xx(i,j+1))+1/d(i); % 给蚂蚁走过的路径添加信息素
end
end
% 打印当前结果
fprintf('第%d轮,最小距离为:%d\n',t,dbest) % 打印当前优化结果
hold off
plot(cityLoc(:,1),cityLoc(:,2),'o','MarkerEdgeColor','k','MarkerFaceColor','y','MarkerSize',10,'LineWidth',2)
hold on
plot(cityLoc([xbest,xbest(1)],1),cityLoc([xbest,xbest(1)],2))
drawnow
% 判断终止条件
last_d = [last_d(2:end),dbest]; % 记录本轮的历史最优值
if((max(last_d)-min(last_d))<delta_goal) % 如果近N轮的优化提升小于阈值
break % 则终止迭代
end % -
end
disp('结果:') % 打印标题
disp(['最优距离dbest = ',num2str(dbest)]) % 打印历史最优目标函数值
disp(['最优路径xbest = ',num2str(xbest)]) % 打印历史最优路径
% 根据行列坐标,从矩阵中获取元素
function y = getMatElement(data,row_idx,col_idx)
row_num = size(data,1);
idx = (col_idx-1)*row_num+row_idx;
y = data(idx);
end代码运行结果如下:
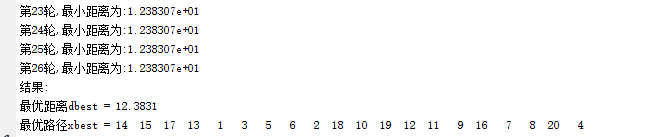
可以看到,经过26轮的迭代,蚁群算法成功找到了较为理想的路径
好了,以上就是蚁群算法的算法流程与代码实现了~
End
 评论
评论