
本站原创文章,转载请说明来自《老饼讲解-深度学习》www.bbbdata.com
转置卷积(transposed-convolution)也称为上卷积(Up-convolution)、反卷积(Deconvolution)
本文讲解转置卷积的基本计算、代码实现,以及转置矩阵的填充、步幅的意义
通过本文,可以快速了解转置卷积是什么,有什么用,以及它的详细计算过程与代码实现方法
本节介绍转置卷积有什么,以及如何计算
什么是转置卷积
转置卷积(transposed-convolution)也称为上卷积(Up-convolution)、反卷积(Deconvolution)
转置卷积在深度学习中常用于对图片进行上采样,即把图片的Size变得更大,如下:
转置卷积也称为反卷积(Deconvolution),但这里的"反"指的是"目的"上的反
卷积可以用于下采样,把图片变得更小,而转置卷积则用于上采样,把小的图片恢复为更大
转置卷积的运算
转置卷积的运算
计算转置卷积时,一般先初始化结果,然后逐列逐行历遍输入的每个元素
每次将当前元素与卷积核相乘,并累加到输出对应位置之中
一个填充为0、步幅为1的转置卷积例子,其计算过程如下:
记输入的大小为,卷积核的大小为
填充0、步幅1的转置卷积,输出大小为:
转置卷积的意义
转置卷积就是把输入的每个元素,按卷积核的大小、权重来广播到周边元素之中
可知,转置卷积是广播自身来达到信息共享,而卷积运算则是吸收周边的元素来达到信息共享
本节介绍转置卷积的填充以及步幅分别是什么
转置卷积的填充
转置卷积的填充(padding),可以理解为反填充,它指的是对输出进行删行象素数
理解转置卷积的填充,不妨直接看一个转置卷积padding的例子:
可知,当padding=1时,就是对输出的周边都删除1像素,即上下各删除一行,左右各删一列
转置卷积的步幅
转置卷积的步幅(stride)指的是每次累加窗口移动的步幅
当步幅为n的时候,置换卷积在每次计算卷积后,会按步幅来进行累加,如下:
直接看一个例子,填充为0,步幅为2的转置卷积的运算结果如下:
可知,当卷积核为2×2、步幅为2×2时,则输出的高宽都是输入的两倍
这就是转置卷积最大的意义,可能通过设置stride,来使输入的Size变大
本节展示转置卷积的代码实现,辅助理解转置卷积
转置卷积-代码实现
下面我们展示在pytorch中调用ConvTranspose2d来计算转置卷积的实现方法
为了深入理解,同时也提供了自行计算转置卷积的计算过程
具体代码如下:
# ---------利用pytorch计算转置卷积---------------
import torch
from torch import nn
X = torch.tensor([[[[0.0, 1.0], [2.0, 0.0]]]]) # 输入x
C = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False) # 初始化转置卷积
C.weight.data = torch.tensor([[[[1.0, 2.0], [3.0, 4.0]]]]) # 初始化卷积核
Y = C(X) # 对X进行转置卷积
print('\n转置卷积计算结果(pytorch):\n',Y) # 打印输出
# ----------自行计算转置卷积-------------------
import torch
X = torch.tensor([[0.0, 1.0], [2.0, 0.0]]) # 输入x
W = torch.tensor([[1.0, 2.0], [3.0, 4.0]]) # 卷积核
Y = torch.zeros((X.shape[0] + W.shape[0] - 1, X.shape[1] + W.shape[1] - 1)) # 初始化输出
for j in range(X.shape[1]): # 对输入逐列
for i in range(X.shape[0]): # 对输入逐行
Y[i: i + W.shape[0], j: j + W.shape[1]] += X[i, j] * W # 累加当前的卷积结果
print('\n转置卷积计算结果(自实现):\n',Y) # 打印输出运行结果如下:
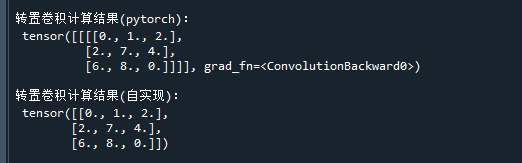
可以看到,自行计算的结果与ConvTranspose2d计算的结果是一致的
转置卷积-填充与步幅-代码
下面展示转置卷积设置padding、stride时,对转置卷积结果的影响
具体代码如下:
# 转置卷积的填充与步幅
import torch
from torch import nn
X = torch.tensor([[[[0.0, 1.0], [2.0, 0.0]]]]) # 输入x
W = torch.tensor([[[[1.0, 2.0], [3.0, 4.0]]]]) # 卷积核
# padding=0,stride=0时的转置卷积
C = nn.ConvTranspose2d(1, 1, kernel_size=2,padding=0, bias=False) # 初始化转置卷积
C.weight.data = W # 初始化卷积核
Y = C(X) # 对X进行转置卷积
print('\n转置卷积结果(padding=0,stride=0):\n',Y) # 打印输出
# padding=1时的转置卷积
C = nn.ConvTranspose2d(1, 1, kernel_size=2,padding=1, bias=False) # 初始化转置卷积
C.weight.data = W # 初始化卷积核
Y = C(X) # 对X进行转置卷积
print('\n转置卷积结果(padding=1):\n',Y) # 打印输出
# stride=2时的转置卷积
C = nn.ConvTranspose2d(1, 1, kernel_size=2,padding=0,stride=2, bias=False) # 初始化转置卷积
C.weight.data = W # 初始化卷积核
Y = C(X) # 对X进行转置卷积
print('\n转置卷积结果(stride=2):\n',Y) # 打印输出运行结果如下:
好了,以上就是转置卷积的介绍与计算方法了~
End
 评论
评论