
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
CART决策树是一个经典的机器学习模型,它具有极强的业务可解释性
本文梳理CART决策树的算法流程,并分析代码实现的难点及解决方案
通过本文,可以了解自实现一棵CART决策树的算法流程,以及相关技术选择
说明:本文CART决策树算法流程的来源
本文是笔者扒取matlab决策树函数fitctree的源码后,梳理整合后得到的CART决策树算法流程,
也就是说,本文中的CART决策树算法流程,就是matlab的决策树函数fitctree的算法流程
而sklearn包中决策树tree.DecisionTreeClassifier与该流程在细节上有所出入,主体上仍然是保持一致的
本节展示CART决策树算法流程图,并说明其中的实现难点
CART决策树-算法流程
根据CART决策树构建过程,整理后可得到CART决策树算法流程
CART决策树算法流程图如下:
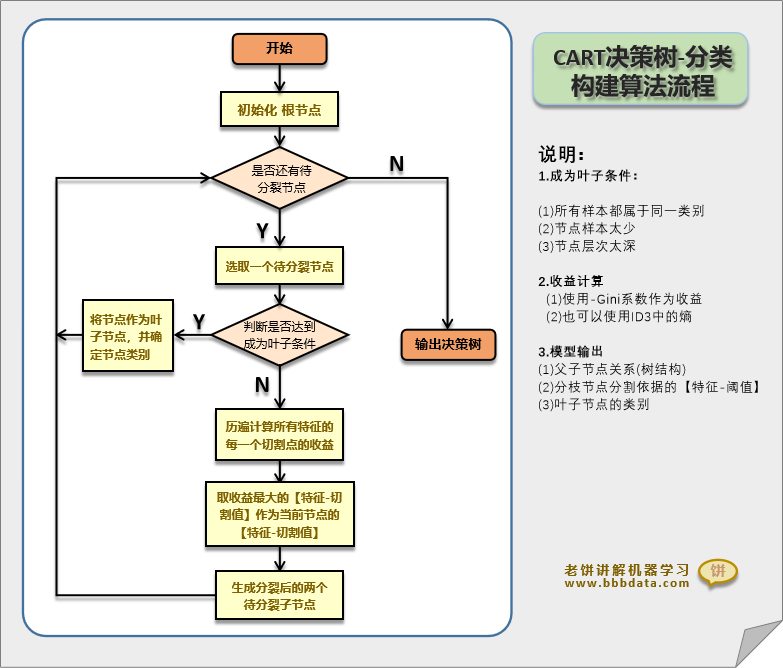
CART决策树的算法流程是非常简单的,
无非就是不断地让未生长的节点继续生长,直到生长完成
😡 代码实现的难点
从CART决策树算法流程图可以看到,CART决策树的实现逻辑是非常简单的,
但真正去编码代码自实现一棵决策树时,会发现有两个难点,如下:
👉 1. 如何表达决策树中树的结构
👉 2. 如何对树进行历遍
本节介绍CART决策树结构的存储方法与树如何历遍
树结构的存储-两种常见方案
目前用于记录决策树的树形结构有两种较常见的方案
第一种是用链表,程序员的至爱,如下:
链表形式的优点是增删时非常方便,缺点是除非画图,不然非常不直观,而且动不动就要历遍
例如要找叶子节点,就需要历遍,要知道有多少个节点,也要历遍
第二种用左右节点编号数组,如下:
用左右节点编号来记录树形结构,看起来没什么毛病,但逻辑上非常不直观
例如在删掉某个节点下所有节点时,处理逻辑就非常绕
树历遍-两种常见方案
树历遍的根本难点在于,历遍过程是动态的,
必须历遍到具体节点,才知道该节点下还有没有子节点
树的历遍也有两个方案: 节点栈方案和递归方案
节点栈方案的处理方式如下:
建立一个节点栈,将未处理的节点放在栈中,每次出栈处理一个节点
处理完当前节点后,把该节点的子节点入栈直到栈中节点数为空,则完成历遍
递归方案的处理方式如下:
递归就是处理函数只要还有子节点,就不断自身调用自身,直到没有待处理的节点
递归的好处是简洁,但代码难理解,而节点栈相对较好理解些,但没有递归简洁
笔者语
由于决策树的实现上存在上述两个难点,注定代码不能简单明了
网上一些看来起简单明了的代码,实则是功能不全的
上面说了,两种存储方式在某些功能上会十分不方便,导致必须用大量代码去把功能堆砌出来
matlab自身是使用 “左右节点编号数组+节点栈的方式”,
而 笔者最终选用“链表+递归”的方式去复现matlab中的算法
主要是笔者需要自行拓展一些功能,以 “链表+递归”更加简洁灵活和方便
具体复现代码见《CART决策树代码(自实现)》
以上就是CART决策树算法流程和实现的全部内容了~
End
 评论
评论