
本站原创文章,转载请说明来自《老饼讲解-机器学习》ml.bbbdata.com
线性回归是一个最简单与最基本的机器学习模型,它用线性关系来拟合样本之间的关系
本文讲解线性回归的模型意义、模型表达式、损失函数,以及它的求解方法和公式
通过本文,可以了解线性回归是什么,以及如何利用最小二乘法、QR分解公式对线性回归进行求解
本节介绍线性回归是什么,以及它的数学表达式
线性回归-模型思想
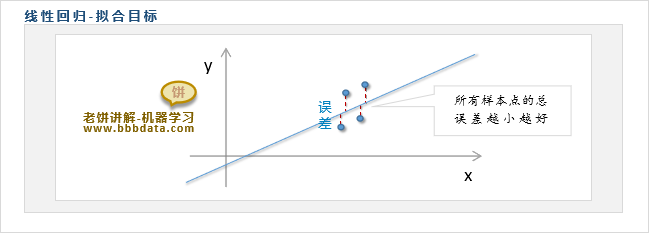
线性回归模型是希望找到一条直线(平面或超平面)去拟合采到的样本数据点,
最佳拟合时,直线与样本的总均方误差最小
几何意义
在x为一维时,y与x组成二维平面,几何意义如下理解
线性回归模型以一条直线拟合数据,如下:
线性回归的拟合目标是总均方误差最小,如下:
线性回归-模型表达式
模型表达式-一般形式
线性回归的模型表达式如下:
线性回归的损失函数为模型预测值与真实值的均方差
线性回归的损失函数如下:
备注:上标 (i) 代表第i个样本,m为样本个数,n为变量个数
模型表达式-矩阵形式
线性回归模型表达式的矩阵形式如下:
备注:这里的X是原变量再加上一列常数1:
线性回归的损失函数的矩阵形式如下:
注意:矩阵形式里对原始X增加了一列常数1
则W比原来的变量多了一个,目的是把 b揉进了W里
本节介绍线性回归模型的求解方法,包括最小二乘法求解和QR分解法
线性回归-最小二乘法求解
线性回归-最小二乘法求解
由于线性回归问题实际就是最小二乘解问题,因此可直接使用最小二乘求解公式进行求解
最小二乘法的求解公式如下:
使用该公式即可求得令损失函数L(W)取得最小值的W
QR分解优化最小二乘解
虽然可以直接使用最小二乘解公式来求解线性回归模型
但实际使用计算机求解时,往往是使用QR分解的方式,避开最小二乘解中复杂的逆矩阵计算
这主要是因为最小二乘解公式需要求的逆矩阵,这样计算较为复杂
什么是QR分解
QR分解是指,将列满秩的矩阵A,分解为正交矩阵Q与上三角矩阵R的积
即:
其中, Q列与列之间两两正交, R为非奇异上三角矩阵
QR分解优化最小二乘法
由最小二乘法的求解公式,与QR分解公式,则有:
由此可得,QR分解方法求解最小二乘解的公式如下:
其中,和由进行QR分解得到
R是一个上三解矩阵,它的逆比的逆更容易求取
注意事项 : 不一定满秩,也就不一定有逆矩阵,以上求解方法将失效
好了,以上就是线性回归模型的原理以及求解方法介绍了~
End
 评论
评论