
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
Fhisher-LDA是一种用于有类别标签数据的降维算法,它是基于最大化瑞利商推导而得的LDA算法
本文讲解Fisher-LDA线性判别的思想和原理,以及Fisher-LDA线性判别的用途和实现例子
通过本文可以快速了解什么是Fisher-LDA,以及如何应用Fisher-LDA于数据降维与类别判别
本节讲解 Fisher-LDA的思想以及模型表达式,快速了解Fisher-LDA是什么
Fisher-LDA是什么
Fisher-LDA全称为Fisher's Linear Discriminant Analysis,即Fisher线性判别分析
Fisher-LDA既可以作为一种变量降维方法,同时也可以作为模型对样本进行类别判别
需要注意的是,它应用于降维时,是需要类别标签y的,是一种有监督学习
Fisher线性判别分析思想出发点
Fisher线性判别分析的思想如下:
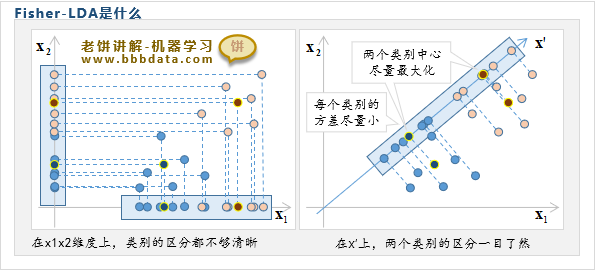
如上图所示,从样本原来的单个维度 或 来看,样本的类别区分度都不够,会混淆在一起
但如果从维来看,两个类别则区分得一清两楚,类别中心的间隔大,每类样本各自聚在一起
因此,Fisher-LDA希望找出新维度,使得样本在新维度的类内方差尽量小,类间方差尽量的大
类内方差则是指每一个类别的样本独自的方差,方差越小则说明每个样本离它的类别中心越靠拢
类间方差是指各个类别中心的方差,方差越大说明各个类别中心离得越开,即各类样本离得越开
这样一来,样本在新维度中,每个类别的区分度都更加清晰
Fisher线性判别模型-数学表述
Fisher线性判别模型(一维)
对于单维度,可易知样本在维度上的投影坐标为 ,则有:
由于希望所有样本在维上的类间方差尽量的大、类内方差尽量小
因此Fisher-LDA采用最大化瑞利商作为的求解目标,如下:
解释:是类间、类内方差比,即类间方差是类内方差的多少倍
最大化这个倍数,自然就能使类间方差尽量比类内方差大
Fisher线性判别模型-多维情况
进一步地,Fisher-LDA不是只找一个新维度,而是找出多个新维度
则对于个新维度,X的投影坐标为,即:
此时,Fisher-LDA的求解目标"最大化瑞利商"则为矩阵形式,如下:
解释:由于 和 都是矩阵,上式用行列式将两者标量化
本节讲解Fisher-LDA是如何进行求解的,以及所求的A的特点
Fisher-LDA的求解-思路
Fisher-LDA通过广义特征值问题来进行求解,具体如下:
一、Fisher-LDA的求解目标
先回顾Fisher-LDA的求解目标,如下:
求一使 最大化
二、引入的广义特征值问题
下面先引入一个广义特征值问题 ,如下:
求一,使得 有非零解
该问题可求得特征值与对应的特征向量
其中,是从大到小排序的
备注:广义特征值问题是一个固有的数学问题,求解原理可参考《》
三、Fisher-LDA的求解问题与广义特征值问题的关系
可证明,Fisher-LDA的求解问题与广义特征值问题的解的关系如下:
1. 广义特征值问题得到的前q个特征向量就是所要求的A
需要注意,这里的前提是都是非0的
如果只有前k个非0,那么则只取
2. A的列维度q小于类别个数K
3. y的类内协方差为单位矩阵,即:
4. y的类间协方差为以为对角元素的对角矩阵,即:
即的类间协方差为
因此,只需要求解上述广义特征值问题就可得到Fisher-LDA所要求的A
本节讲解Fisher-LDA是如何应用于分析、变量降维与类别判别
Fisher-LDA的成份贡献与分析
Fisher-LDA的成份贡献
对于变换后的第i维变量,它的类间协方差代表了它所包含的"区分样本类别"的信息
因为类间协方差就是各类别样本中心的方差,方差越大说明类别的区分度越大,如下:
不妨把变换后的各个称为判别成份(component),其类间协方差占比称为成份贡献
由于各成份的类间协方差为,可知第i个成份的贡献为:
备注:强调一下,由于,所以
成份贡献代表了该成份包含了X中多少"用于区分类别"的信息,贡献越大则成份越重要
Fisher-LDA判别分析
进一步地,我们可以将Fisher-LDA理解为:
从X中抽出一个一个的"类别信息"成份,每个成份包含了一部分X中蕴含的类别信息
因此,不管X有多少维,真正有用的是它所包含的"类别判别信息"
我们只需使用Fisher-LDA抽出它的判别成份,进一步地,对判别成份y进行分析即可
例如,X蕴含的类别信息共由几个判别成份组成,每个成份的贡献各占多少等等
Fisher-LDA用于降维
Fisher-LDA降维
由于Fisher-LDA模型中的A最多只有K-1列,因此用A进行变换后的 也只有K-1列
即通过Fisher-LDA的变换后,X将会被降维到K-1维
直观的理解,y只是抽取了X中"能区分类别"的信息成份,因此y的维度更小
Fisher-LDA根据贡献进行降维
由于成份贡献代表了一个判别成份里包含了多少X中用于区分类别的信息
因此,我们可以通过忽略掉一些贡献过少的判别成份,从而起到进一步降维的作用
由于,即的贡献由大到小
所以在实际操作中只需根据,来截取A的前k列,就可降到k维,如下:
✍️直观理解为什么维度最大等于K-1
为什么Fisher-LDA降维后,其维度最大等于K-1(K为类别个数)呢?
这主要是因为Fisher-LDA只抽取了X中关于类别的信息,即样本各个类别中心的信息
如上图所示,两个类别中心只需一维就能表示它们的位置关系,三个类别中心则要两维
同理,K个类别中心需要K-1维,因此Fisher-LDA降维后只需K-1维就能表示X中有关类别的信息
Fisher-LDA用于类别判别
由于LDA变换后的数据的类内协方差矩阵为单位矩阵
则适用于《贝叶斯判别函数》中类内协方差为时的一次判别形式
即样本的类别判别函数如下:
其中,:第k行是第k类的样本均值
:K维列向量,为类别k的先验概率
一般用第k类样本在总样本的占比 来作为
判别函数的输出是一个K维列向量,第k个元素代表样本属于类别k的判别值
使用上述判别函数得到各类别的判别值后,再将判别值最大的类别作为预测类别
本节展示一个Fisher-LDA的具体实现例子,进一步了解如何使用Fisher-LDA
Fisher-LDA代实现实例子
下面展示一个使用sklearn实现Fisher-LDA用于降维与判别的例子
代码实现如下:
'''
sklearn使用Fisher-LDA的例子
'''
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
#加载数据
iris = datasets.load_iris() # 加载iris数据
X = iris.data # 用于建模的X
y = iris.target # 用于建模的y
target_names = iris.target_names # 各个类别的名称
#------------Fisher-LDA线性判别模型训练与预测-----------------
#
lda = LinearDiscriminantAnalysis(n_components=2,solver='eigen') # 初始化Fisher-LDA(eigen代表是Fisher-LDA),n_components代表降到多少维
clf = lda.fit(X, y) # 训练LDA模型
Xt = clf.transform(X) # 用训练好的LDA对数据进行降维
pred_y = clf.predict(X) # 用训练好的LDA进行类别预测
#------------打印结果-----------------
#降维函数transform就是X@clf.scalings_[:,:n_components]
#判别函数predict 就是(X@clf.coef_.T+clf.intercept_).argmax(axis=1)
print('\n变换矩阵A=',clf.scalings_) # 变换矩阵A,A的列并不全是有效的,只有前K-1列有效,K是类别个数
print('\n各维贡献占比=',clf.explained_variance_ratio_) # 贡献占比
print('\n判别模型系数=',clf.coef_) # 用于判别的模型系数
print('\n判别模型阈值=',clf.intercept_) # 用于判别的阈值
# 各类别在降维后(新特征空间)的样本分布
plt.figure() # 初始化画布
colors = ["navy", "turquoise", "darkorange"] # 设置颜色
for color, i, target_name in zip(colors, [0, 1, 2], target_names): # 逐类别画出样本点
plt.scatter(Xt[y==i,0],Xt[y==i,1],color=color,label=target_name) # 画出样本点,并以颜色标示类别
plt.legend(loc="best", shadow=False, scatterpoints=1) # 设置图例
plt.rcParams["font.sans-serif"] = ["SimHei"] # 设置中文
plt.rcParams['axes.unicode_minus'] = False # 设置坐标轴负号显示方式
plt.rcParams["figure.figsize"] = (9, 4) # 设置figure_size尺寸
plt.title("各类别在降维后(新特征空间)的分布") # 设置标题
plt.show()运行结果
运行结果如下:
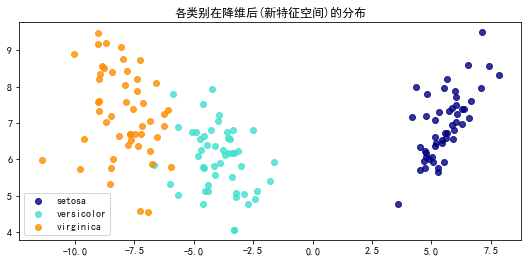
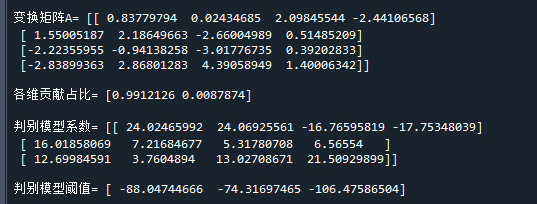
从图中可以看到,进行Fisher-LDA转换后,在横轴就已经能很好地区分类别了,而纵轴则没什么区分
从各维贡献占比也可以看出,第一维的类别信息贡献已经达到了99%,第二维只有0.8%,基本没什么用
因此,在该例中,其实只需要一维,就足以表示类别信息了
好了,以上就是Fisher-LDA线性判别分析的基本思想、原理以及具体代码实现了~
End
 评论
评论