本站原创文章，转载请说明来自《老饼讲解-BP神经网络》www.bbbdata.com
本文讲述BP神经网络的数学表达式，
通过数学表达式，可以更清晰、具体、直观地了解BP神经网络背后的意义，使BP神经网络不再抽象
理解BP神经网络的数学表达式，可以说是正式踏入理解BP神经网络的第一步
在这里，我们先用一个简单例子，讲述BP神经网络的数学表达式，
通过本例可以形象地知道BP神经网络拓扑图与数学表达式的对应关系
BP神经网络-例子配置
现有一个BP神经网络，它的结构如下
1、一个输入层，一个隐层，一个输出层， 输入层、隐层、输出层的节点个数分别为 [2 ，3，1]
2、传递函数设置：隐层（ tansig函数），输出层（purelin函数）
相对应的模型拓扑图如下
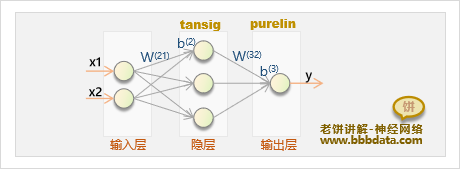
BP神经网络的数学表达式
对于上述的BP神经网络例子，可以根据模型写出模型的数学表达式如下
可以看到，BP神经网络的数学表达式中参数很多，
但实际只有两类参数：权重w和阈值b
代表这个权值是第2层的第2个节点到第3层的第1个节点的权值
代表这个阈值是第2层的第1个节点的阈值
备注：权重矩阵w的下标，一般由后层到前层，这样在矩阵表述时更为简洁
本节讲解BP神经网络权重、阈值的矩阵形式
BP神经网络-三层结构的数学表达式的矩阵形式
对于三层BP神经网络的表达式，写成通用的矩阵形式为
这里的为矩阵，和为向量，
上标和分别代表输出层(out)和隐层(hide)
✍️备注
权重矩阵的第一个下标是下层的神经元索引，第二个下标 i 才是前层索引
如下：
3输入，4隐节点，2输出为例，
各个w、b的size可以图解如下：
对于多层的BP神经网络的数学表达式，也是类似的思路,不再讲述
以上就是BP神经网络的模型数学表达式的全部内容了~
End
