
本站原创文章,转载请说明来自《老饼讲解-机器学习》www.bbbdata.com
本文讲解什么是SVD降维,并且分析SVD降维的本质和原理
从本文可以了解SVD降维的使用流程,并从几何意义上形象掌握其本质
SVD分解简单回顾
SVD分解是指对矩阵A作如下分解 :
m*n矩阵A,将其分解为、 和 三个矩阵,如下
其中,
是m*m的酉矩阵
是m*n半正定对角矩阵
是n*n的酉矩阵
(1) 通常 对角元素由大到小排序,这样 、和是唯一的
(2) 对角线上的元素称为A的奇异值
本节讲解什么是SVD降维,该怎么使用与操作
SVD降维及操作流程
要了解什么是SVD降维,不必看太多文字描述,
直接看一下它的流程就能自然明白
SVD降级操作流程
1.对目标矩阵A进行SVD分解
得到 和 三个矩阵
即
2.根据对角元素的大小来决定k的取值
即如果值较小,则只取前面k个值,
从而获得近似矩阵A'
3. 用 和替代进行存储,因为与近似,
而可以拆解成和进行记录,它们的记录量比直接记录A更加少
从而起到压缩的效果,这就是SVD降维
✍️为什么记录量更加少
为什么记录和比直接记录A更加少?
不妨看下两者所需的记录量
(1) 存储A需要存储数字个数:
(2) 存储和 需要存储数字个数:
所以当k较小时,后者就比前者要小
SVD降维实例
例如一张图片349*284像素,直接记录的存储量为349*284=99116,
对它进行SVD分解,在k取不同值时,图片的质量如下: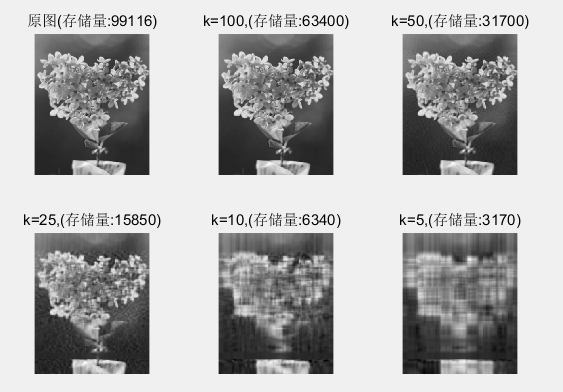
可以看到,当k=50时,
它的存储量为31700,只有原图的1/3
但图片质量也仍在可接受范围内
本节从数值及几何角度,分析为什么去掉小的σ对原矩阵影响不大
从而更形象深入理解SVD降维是怎么一回事
SVD降维原理分析-数值角度
从数值角度分析,为什么通过SVD分解后,
去掉较小的奇异值会是原矩阵的近似
单列分析
由 SVD分解得
单看A的第 j 列(简记的第 j 列为v):
可以看到,A每一列都为U前n列线性组合而成
去掉小的σ 对A单列的影响
当很小的时候,也就很小
注意:U和V都是酉矩阵,所以U和V的元素都
假设第k个之后的都很小,
那么就很小,
也即
矩阵形式即为:
其中
指U的前k列
指 的前k行前k列
为 的前k行
去掉小的σ对A的影响
如果每列都取近似值,则为
其中,
指U的前k列
指 的前k行前k列
指 的前k行 发
因此,是A的近似值,去掉小的σ对A的影响不大
SVD降维原理分析-变换角度
从变换角度分析,为什么通过SVD分解后,
去掉较小的奇异值会是原矩阵的近似
A作为变换的过程
将A 作为一个变换来看待,
它把V(n*n空间)的每个基变换为U(m*m空间)的n个基,
并作对应的伸缩
现有一x,A对x变换的过程等同如下:
A在对x变换之前,我们把x分解到V的n个基上,
再通过V的n个基变换到U的n个基,并自作伸缩,
在U上再重新组合,即得到最后的变换结果
见《SVD分解》
A的近似变换
在A对x变换过程中,
把 x 分解到V的基后,V的基变换到U的基中,
有一些较小的基,在变换之后,也会非常小
在U中重新组合时,这些小的基对变换结果影响甚微
如果我们可以忽略这些小的基,那么得到的是一个近似的变换结果
也即V基变换到U基中,只保留较大的,而把较小的置0
则这个近似变换A'的变换表达则为:
,
其中,是把对角元素中较小值置0后得到
近似变换的表达简化
设对角第k个元素之后都为0,
0元素对乘积结果无影响,去掉对应的行列,
则有
其中,
指U的前k列,即U变成m*k矩阵
指的前k行前k列,即 变成k*k矩阵
则是 的前k列,即 变成了n*k矩阵
End